Tag: monte carlo

New Charts for the Probabilistic View

A couple of months ago, Election Graphs added charts showing how the odds of candidates winning each state evolved. Since then we have referred to those odds quite a bit, and have also discussed how I can combine those individual state by state odds through a Monte Carlo simulation.

I started doing those simulations offline and occasionally reporting results based on that here on the blog. But these were still only manual simulations I was doing offline. Nothing on the ElectionGraphs.com pages for Election 2020 showed this.

Well, a couple of weekends ago, I fixed that, and have done a bit of debugging since, so it is ready to talk about here. I have started with the comparison page where you can look at how various candidate pairs stack up against each other.

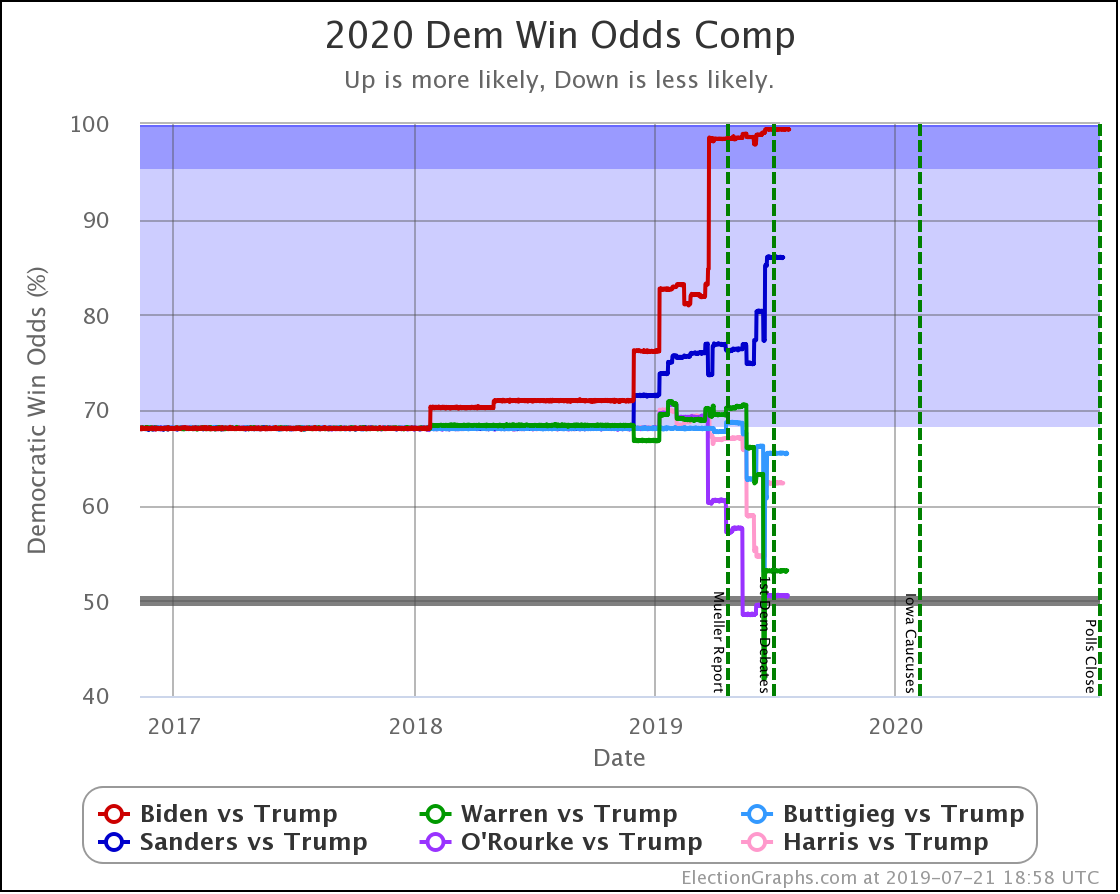
Here is the key chart:

This chart shows the evolution over time of the odds of the Democrats winning as new state polls have come in. The comparison page also shows graphs for the odds of a Republican win, if you prefer looking at things from that point of view. Those two don't add up to 100% because there is of course also a chance of a 269-269 electoral college tie, and there is also a chart of that. Together the three will add to 100%.

The charts are automatically updated as I add new polls to my database.

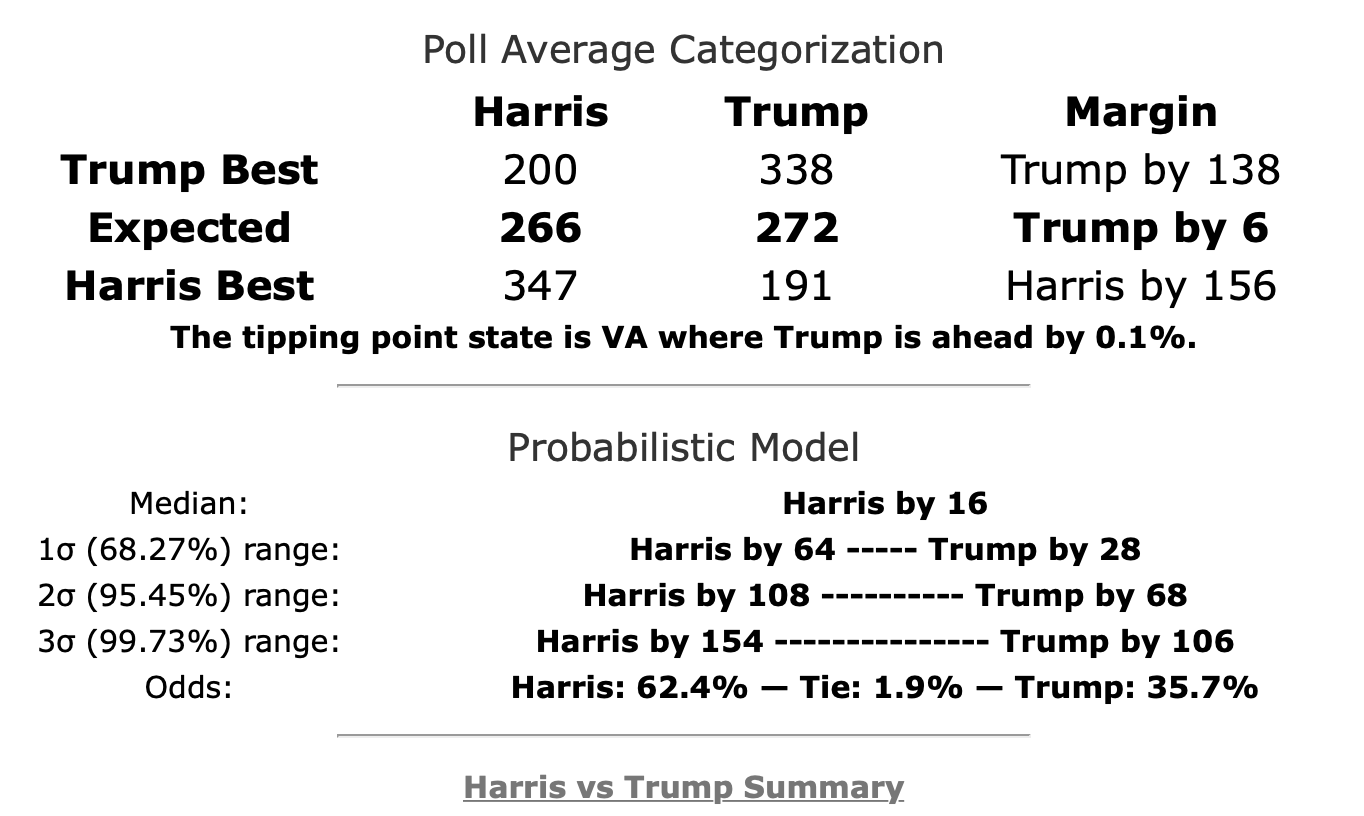
The summary block for each candidate pair on the comparison page has also been updated to include the win odds information:

For the moment this is only on the comparison page, not on the individual candidate pages. This summary also contains more detail than is available in the graphs at this point. I will be adding more charts to close that gap when I get a chance.

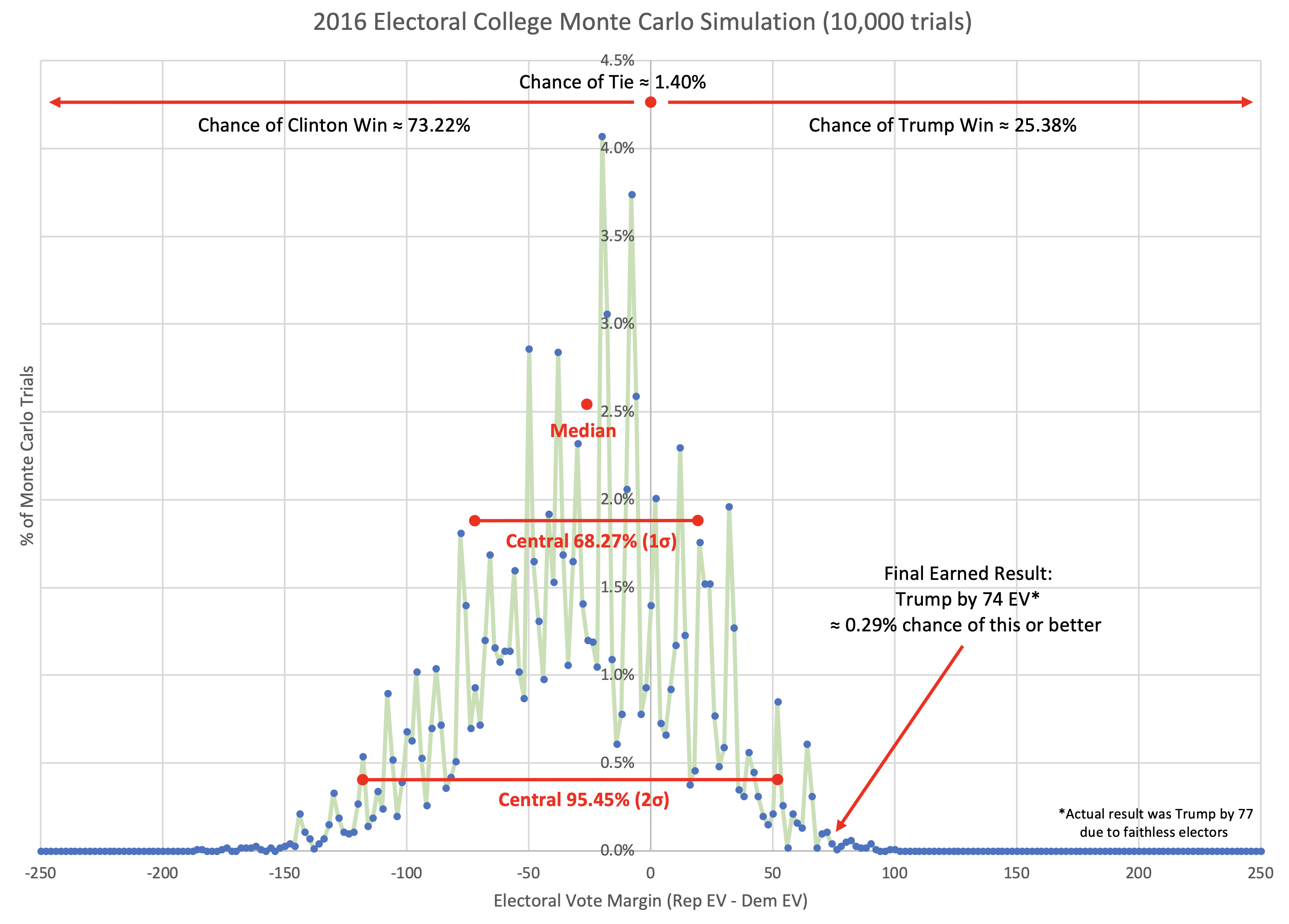
I've used the Harris vs. Trump summary as the example here because it (along with O'Rourke vs. Trump) contains something curious that requires a closer look. Namely, you'll notice that the "Expected" scenario (where every candidate wins all the states where they lead in the poll average) shows a different winner than the "Median" scenario (the "center" of the Monte Carlo simulations when sorted by outcome).

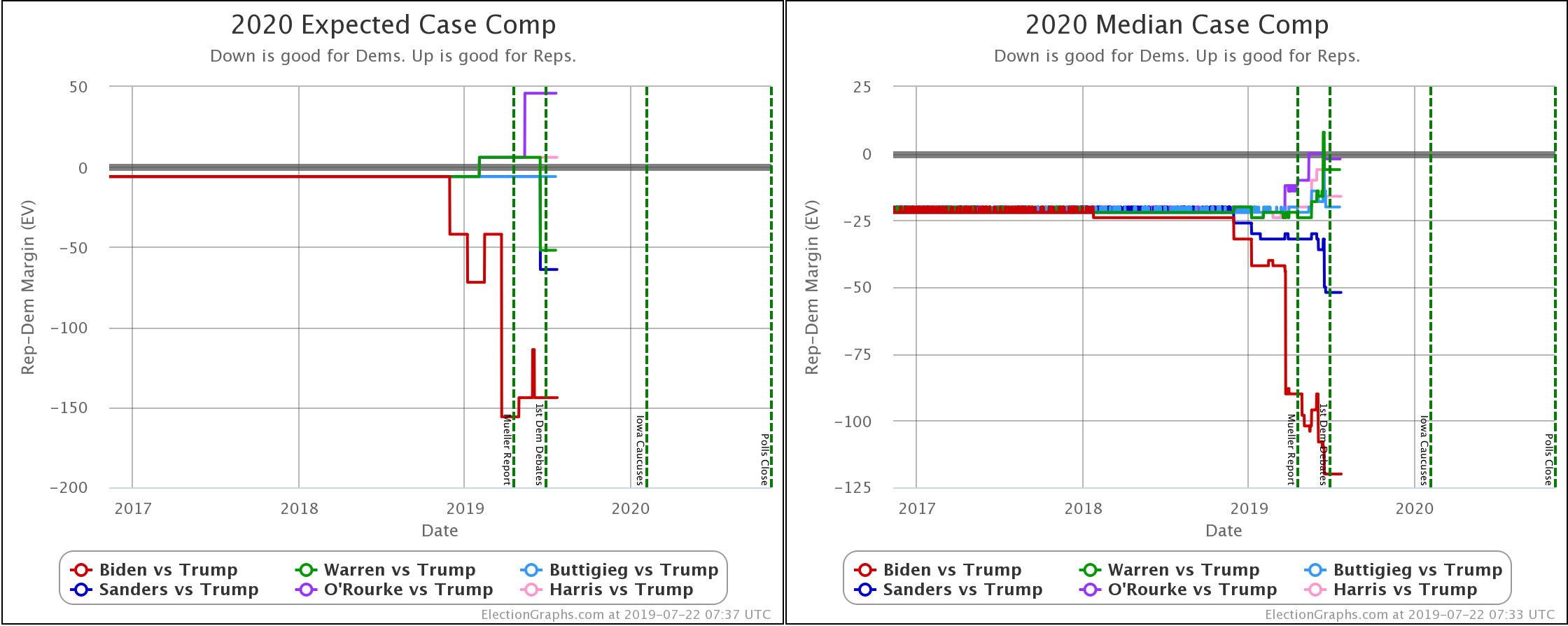
When you look at the charts for the expected case vs. the median case, it is evident that the median in the Monte Carlo simulations does not precisely track the expected case. In fact, in some instances, the trends don't even move in the same direction. So what is going on here?

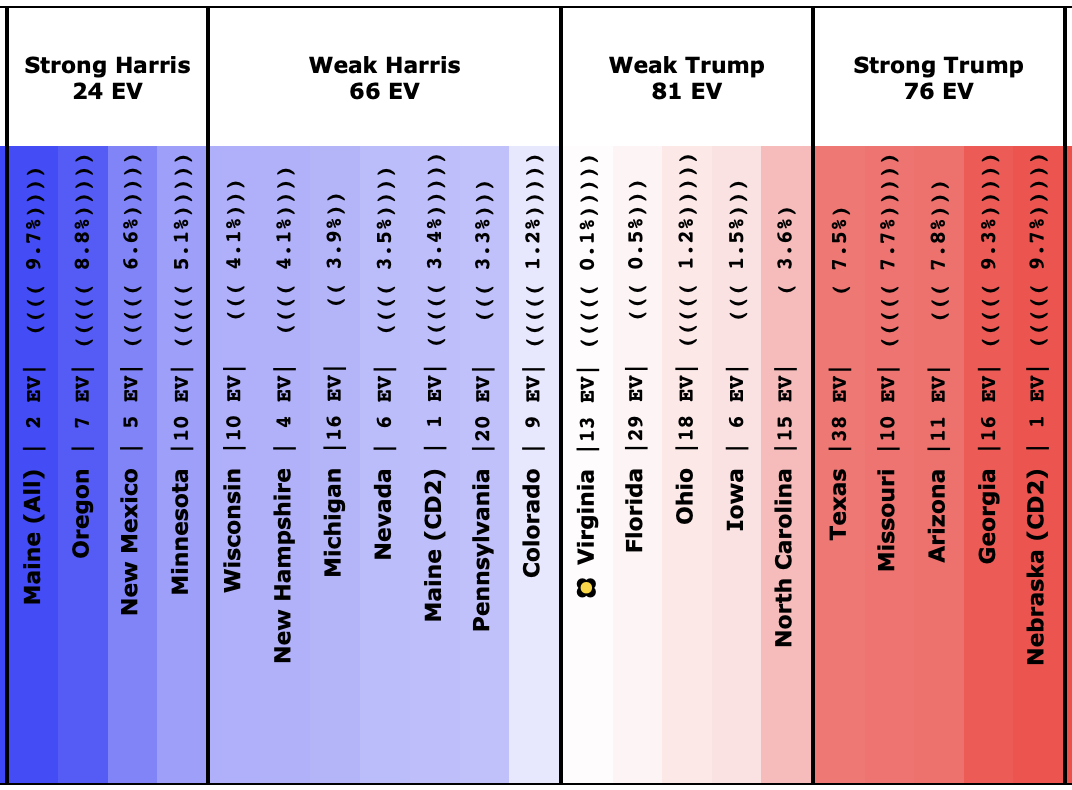
It would take some detailed digging to understand specific cases, but as an example, a quick look at the spectrum of the states for Harris vs. Trump can get some insights.

Now, I don't currently have a version of this spectrum showing win odds instead of the margin, but without that, you can still immediately see why even though Trump leads by six electoral votes "if everybody wins the states they lead", Harris might win in the median case in a simulation that looks at the situation more deeply.

The key is the margins in the swing states. With only a six electoral vote margin, it only takes three electoral votes flipping to make a 269-269 tie, and 4 to switch the winner.

Fundamentally, there are four "barely Trump" states that have a good chance of ending up going to Harris, but only one "barely Harris" jurisdiction that has a decent chance of going to Trump.

Looking at the details:

Trump's lead in Virginia's (13 EV) poll average is only 0.1%, which translates into a 44.9% chance of a Harris win.

Trump's lead in Florida's (29 EV) poll average is only 0.5%, which translates into a 40.2% chance of a Harris win.

Trump's lead in Ohio's (18 EV) poll average is only 1.2%, which translates into a 30.9% chance of a Harris win.

Trump's lead in Iowa's (6 EV) poll average is only 1.5%, which translates into a 28.4% chance of a Harris win.

Those are all the states with a Trump lead where Harris has more than a 25% chance of winning the state. Harris only needs to win ONE of those states to end up winning nationwide. Doing the math, if the odds of winning are independent (which is not strictly true, but is probably a decent first approximation), there is an 83.7% chance that Harris will win at least one of these four states.

Now, there is one Harris state where Trump has a greater than 25% chance of winning. That would be Colorado, where Harris leads by 1.2%, which translates into a 41.6% chance of a Trump win. So that compensates a bit.

But in the end, with this mix of swing states, Harris wins more often than she loses in the simulations (62.4% of the time), and the median case is a narrow 16 EV Harris win.

The straight-up "if everybody wins all the states they are ahead in" expected case metric is a decent way of looking at things as far as it goes. Election Graphs has used it, along with the tipping point, as the two primary methods of looking at how elections are trending in the analysis here from 2008 to 2016. And it has done pretty well. In those three elections, 155/163 ≈ 95.09% of races did indeed go to the candidates who were ahead in the poll average. That view has the advantage of simplicity.

But the Monte Carlo simulations (using state win probabilities based on Election Graph's previous results) give a way of quantifying how often the underdog wins states based on the margin, and how that rolls up into the national results. It can catch subtleties that are out of reach if you only look at who is ahead.

So from now on, Election Graphs will be looking at things both ways. The site will still have the expected case, tipping point, and "best cases" gotten from simply classifying who is leading and which states are close. But we'll also be looking at the probabilistic view. We may be looking at things the new way a bit more. But they will both be here.

Right now that information is on the national comparison page, the state detail pages, the state comparison pages, and the blog sidebar. There is still nothing about the probabilistic view on the candidate pages. That is next on the list once I get some time to put some things together.

469.6 days until polls start to close.

Stay tuned.

For more information:

This post is an update based on the data on the Election Graphs Electoral College 2020 page. Election Graphs tracks a poll-based estimate of the Electoral College. The charts, graphs, and maps in the post above are all as of the time of this post. Click through on any image to go to a page with the current interactive versions of that chart, along with additional details.

Follow @ElectionGraphs on Twitter or Election Graphs on Facebook to see announcements of updates. For those interested in individual poll updates, follow @ElecCollPolls on Twitter for all the polls as I add them. If you find the information in these posts informative or useful, please consider visiting the donation page.

Predicting 2016 by Cheating


This is the fourth in a series of blog posts for folks who are into the geeky mathematical details of how Election Graphs state polling averages have compared to the actual election results from 2008, 2012, and 2016. If this isn’t you, feel free to skip this series. Or feel free to skim forward and just look at the graphs if you don’t want or need my explanations.

You can find the earlier posts here:

The 2016 states we got wrong

In the last post I used the historical deltas between the final Election Graphs polling averages in 2008-2016 to construct a model that given a value for a poll average, would produce an average and standard deviation for what we could expect the actual election results to be. So what can we do with that?

I don't have another election year with data handy to test this model on. No 2020, no 2004, no 2000, no earlier cycles either. So I'm going to look at 2016, even though I shouldn't.

Just as examples, lets look at what the odds this model would have given to the states Election Graphs got wrong in 2016… This technically isn't something you should do, since we are using a model on data that was used to construct the model, which isn't cool, but this is just to get a rough idea, so…

 Final AvgDem Win%Rep Win%Actual
WID+7.06%
98.76%1.24%R+0.77%
MID+2.64%70.59%29.41%R+0.22%
ME-CD2D+2.04%67.92%32.08%R+10.54%
PAD+1.59%66.27%33.73%R+0.71%
NVR+0.02%45.85%54.15%D+2.42%

The only one that is really surprising is Wisconsin, just as it was on Election night in 2016. Every other state was clearly a close race, where nobody should have been shocked about it going either way.

Wisconsin though? It was OK to be surprised on that one.

OK, and maybe the margin in ME-CD2, but not that Trump won it.

Doing some Monte Carlo

Let's go a bit farther than this though. One thing Election Graphs has never done is calculate odds. The site has provided a range of likely electoral college results, but never a "Candidate has X% chance of winning". But with the model we developed in the last post, we now have a way to generate the chance each candidate has of winning a state based on the margin in the poll average, and with that, you can run a Monte Carlo simulation on the 50 states, DC, and five congressional districts.

Now, once again, it is kind of bogus to do this for 2016 since 2016 data was used to construct the model, but we're just trying to get an idea here, and we'll just recognize this isn't quite a legitimate analysis.

So, here is a one off running the simulation 10,000 times to generate some odds. I'd probably want a bit larger number of trials if I was doing this "for real". I might also smooth the win chances curve in the last post to get rid of some of the jaggy bits before using it as the source of probabilities for the simulation. And obviously if you ran this again, you'd get slightly different results. But here is the result of that one run with 10,000 trials…

Well, that is a fun graph. It puts the win odds for Trump at 25.38%.

Now, I emphasize again that this is cheating. Because the facts of Trump's win are baked into the model. We're testing on our training data. That's not really OK. Having said that though…

How does this compare to where other folks were at the end of 2016? I looked at this in my last regular update prior to the results coming in on election night, so here is my summary from then:

So this Monte Carlo simulation using the numbers calculated as I have described would have given Trump better odds than anybody other than FiveThirtyEight. Again though, I am cheating here. A lot.

But here is the thing. Even though I would be giving Trump pretty good odds with this model, the chance of him actually winning by as much as he did (or more) is actually still tiny at 0.29%. With these odds a Trump win should not have been a surprise, but a Trump win by as much as he actually won by… that still should have been very surprising.

Comparisons

In this series of posts, we've been looking at a whole bunch of different ways of answering the basic question "what is a close state?". One reason I am looking at this is that the way Election Graphs has done our "range of possibilities" in the past is just to define what a close state is, and then let all of them swing either to one candidate or the other, and see what the range of electoral college results would be.

So lets see what electoral college ranges we would have gotten in 2016 with each of the methods I've gone over in the last few blog posts:

The two showing the ranges from the Monte Carlo simulation are dimmed out because they are determined by a completely different method, not swinging all close states back and forth.

It is interesting that both the 1 sided and 2 sided histogram 1σ boundaries would end up with the exact same boundaries as my current 5% bounds. But as you can see there are a ton of different ways to define "too close to call" which result in a huge variation on how the range of possibilities gets described.

So what to do for 2020? How will I define close states?

You'll have to wait a little longer for that.

Before I get to that, it is also worth looking at the national race as opposed to just states. On Election Graphs I have used the "tipping point" to measure that. What tipping point values should be considered "too close to call"?

I'll look at that in the next post….

You can find all the posts in this series here: