Election Graphs

Welp, I seem to have gotten into a pattern of a blog update every 50 days, even though in my head I was aiming for every 28 days at this point. The last two posts were when there were about 500 and 450 days until the election, now there are about 400. Oops.

Posts will still accelerate as we get closer to the election of course, but the main place you should be looking for the current situation is not these blog posts anyway, it is the 2024 Electoral College page. That is updated regularly whenever new state level polls come out. At this point that is generally at least once a week, and often more frequently than that.

Because of that, I actually have now switched things around so if you just go to electiongraphs.com you will now end up there instead of the blog. You can always click through to the blog if you want, where I'll post occasional posts like this one summarizing how things have evolved lately. But you can see that from the graphs yourself too of course.

OK, before I go through the details of how things have changed over the last 50 days, here is the quick summary for those who don't want to read the rest:

• If a Biden vs Trump election was held today, it would still be a dead heat and could easily go either way. A ton of critical states are "too close to call".
• Biden has a narrow lead if you take the polls at face value, but given that on average in the last four election cycles polls have tended to underestimate the Republican, I still give Trump a slight edge on the probabilistic views.
• From November until June the trend was in Biden's direction. But some polls I added in August, which covered late June dates, bounced things back in Trump's direction a bit, and things have been pretty steady since then.

OK, now for all the detail for folks who want it.

I'm not going to count and list all the individual polls that have been entered since the last update like I have before. Takes too much time. For those who just want to see a list of all the polls, look here.

If you want updates on each and every poll as it comes out, as well as daily summaries of the status for the best polled matchup (currently Biden vs Trump), follow Election Graphs on Mastodon.

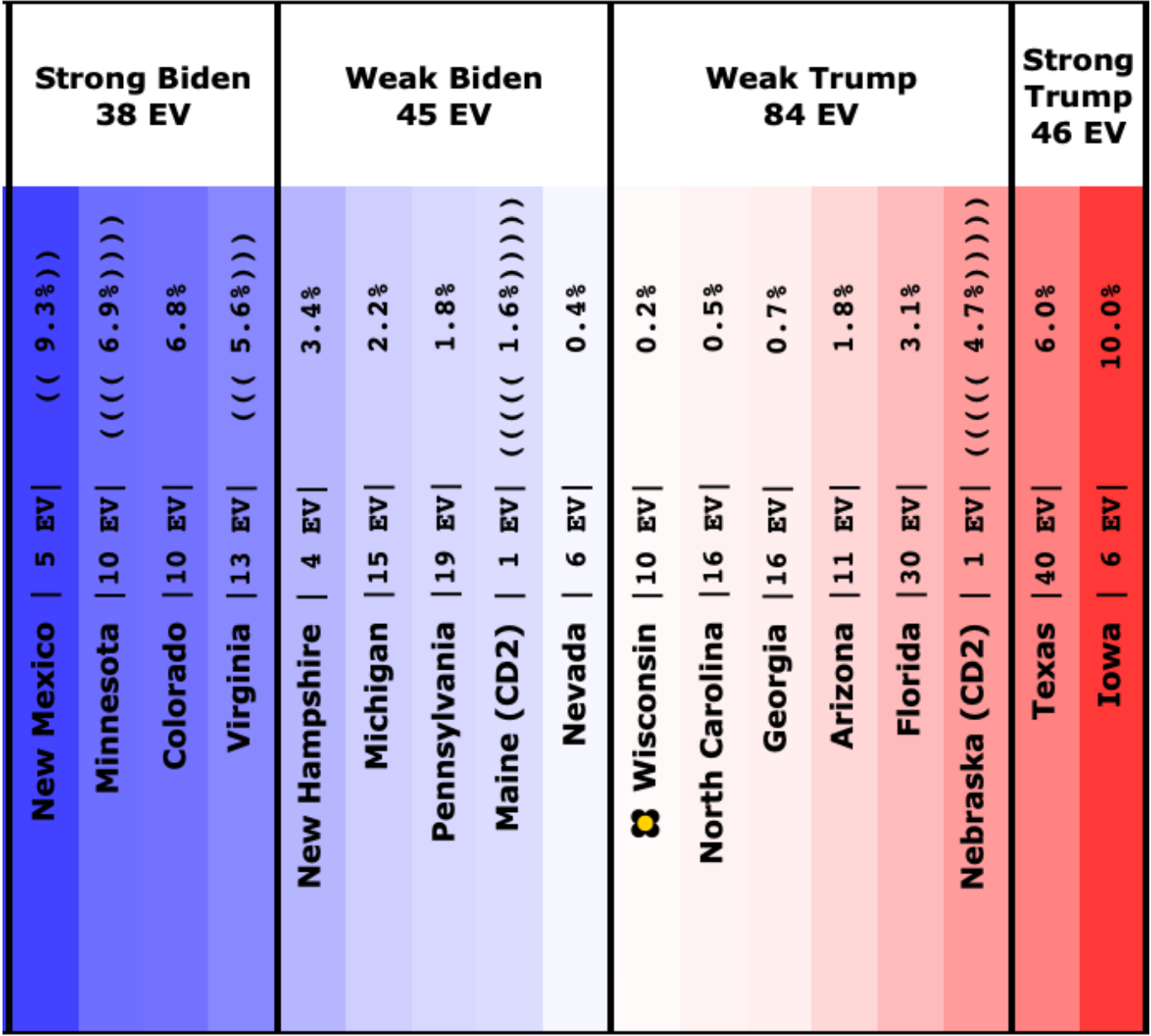
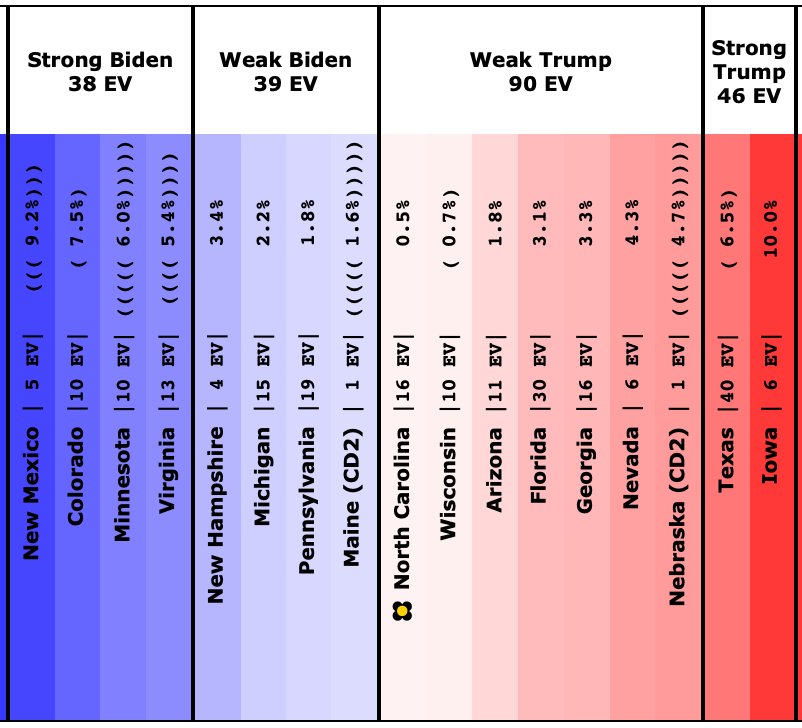
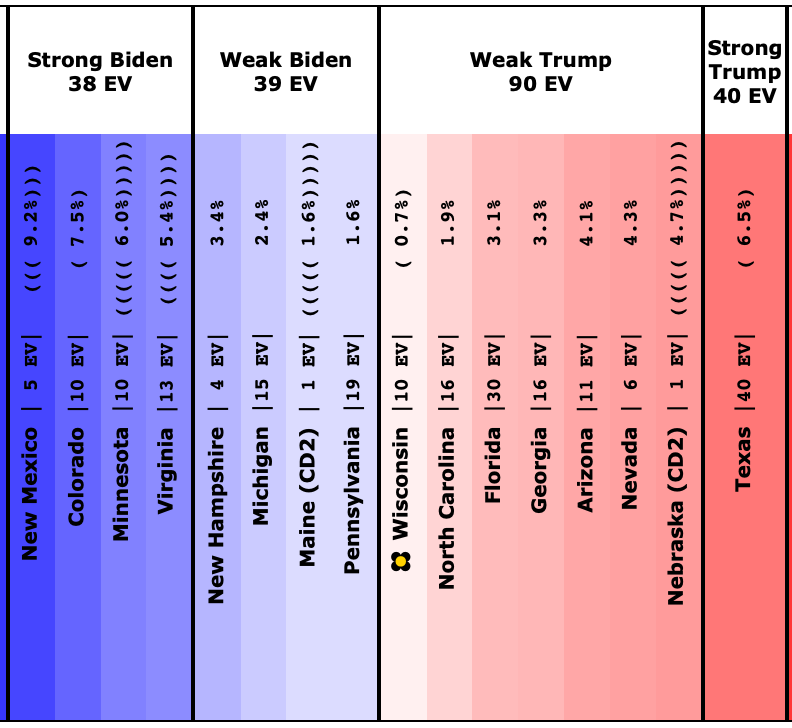
OK, so to get started, we will look at how the spectrum of close states has changed.

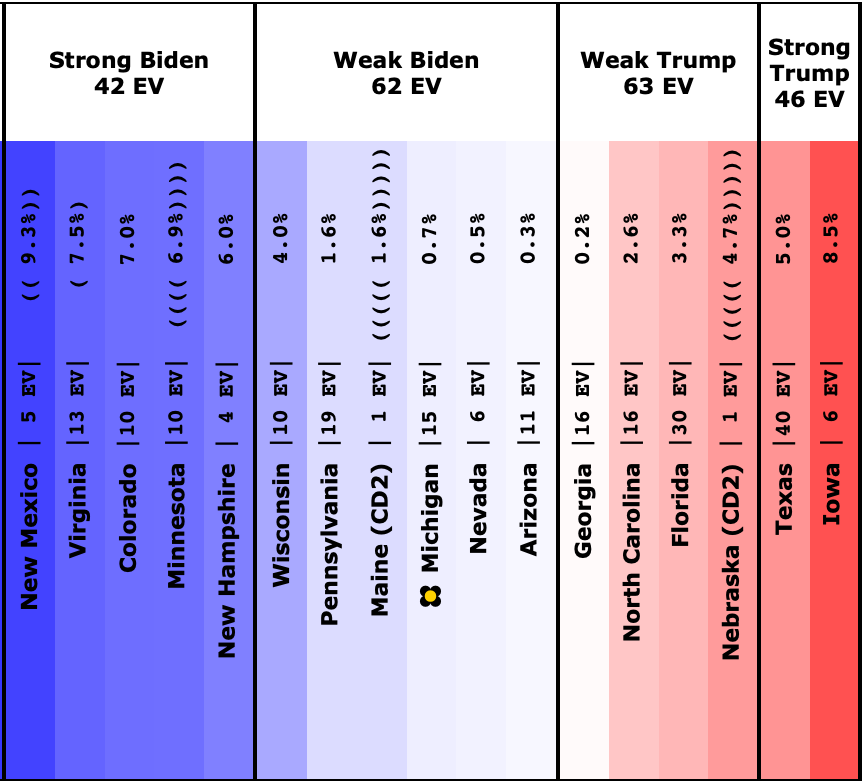
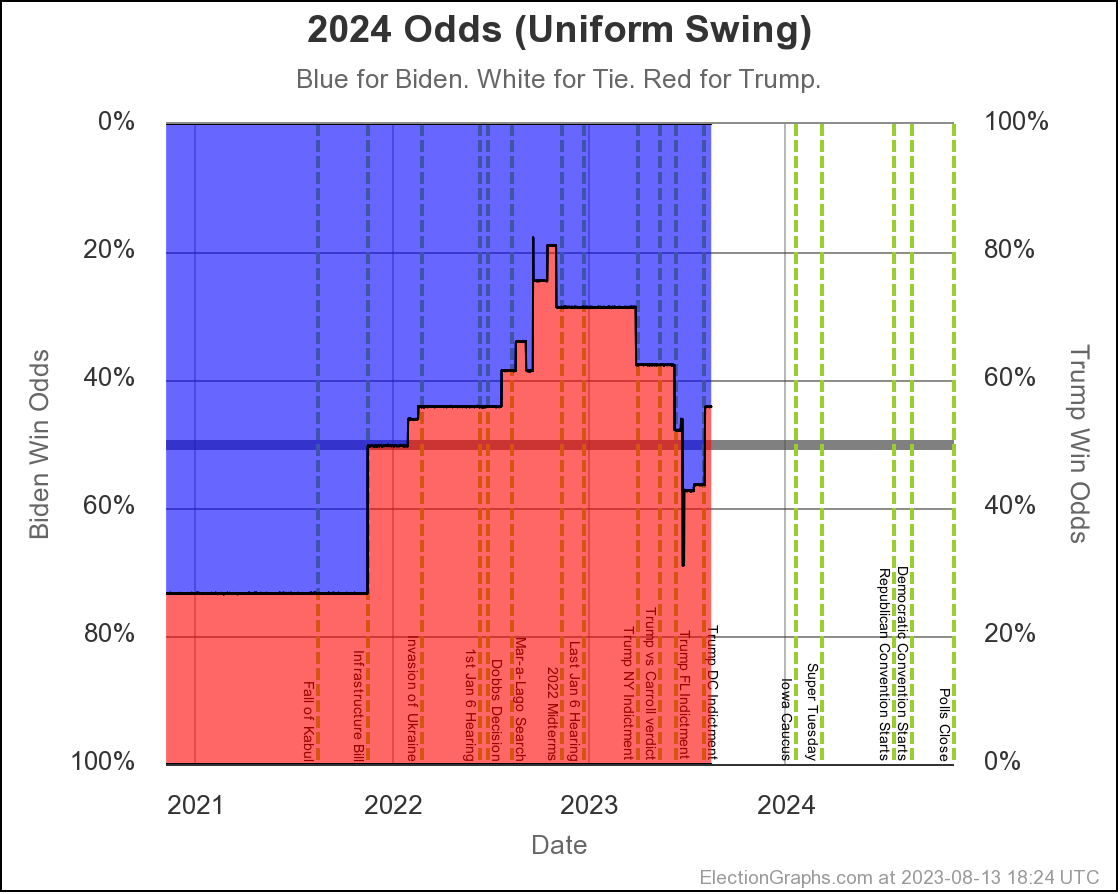
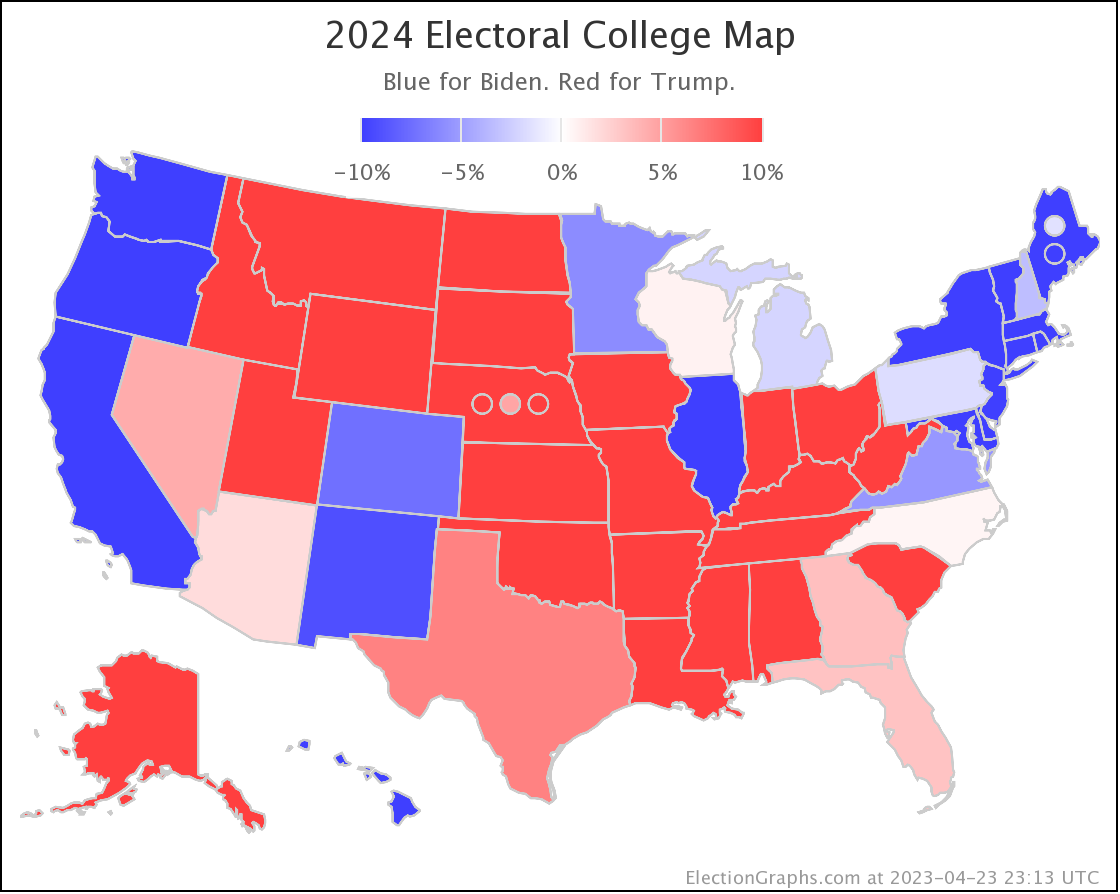
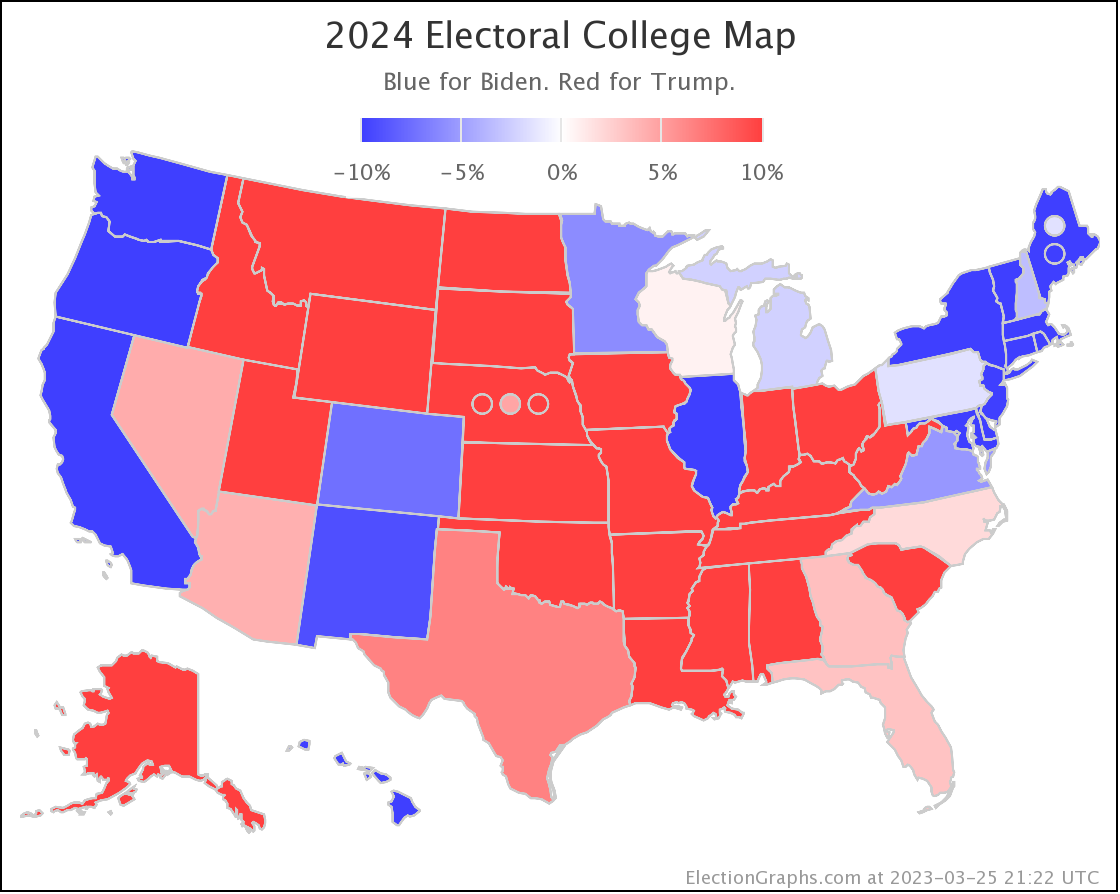
This is how it looked when I did the last blog post on 2023-08-13:

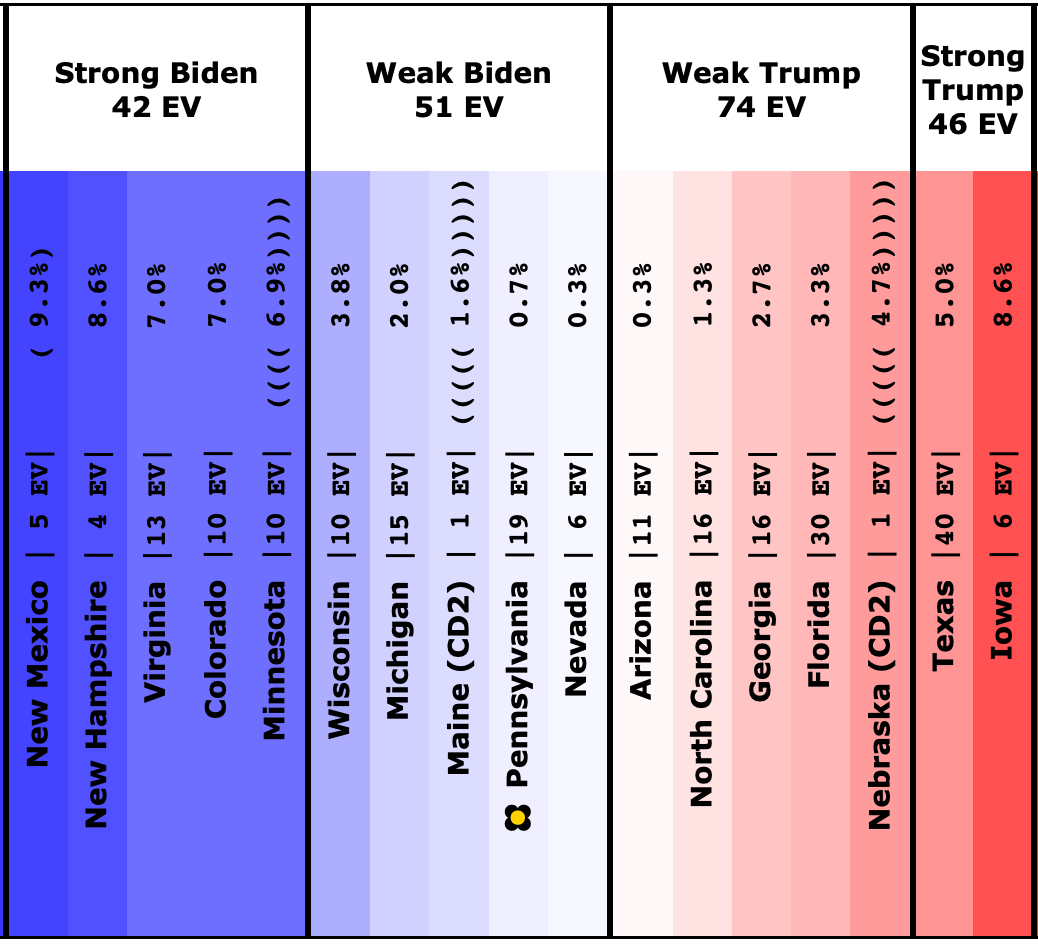
And here is how it looks now on 2023-10-02:

The states where the poll average moved toward Trump are:

• Pennsylvania (19 EV): Biden by 1.6% -> Biden by 0.7% (Trump+0.9%)
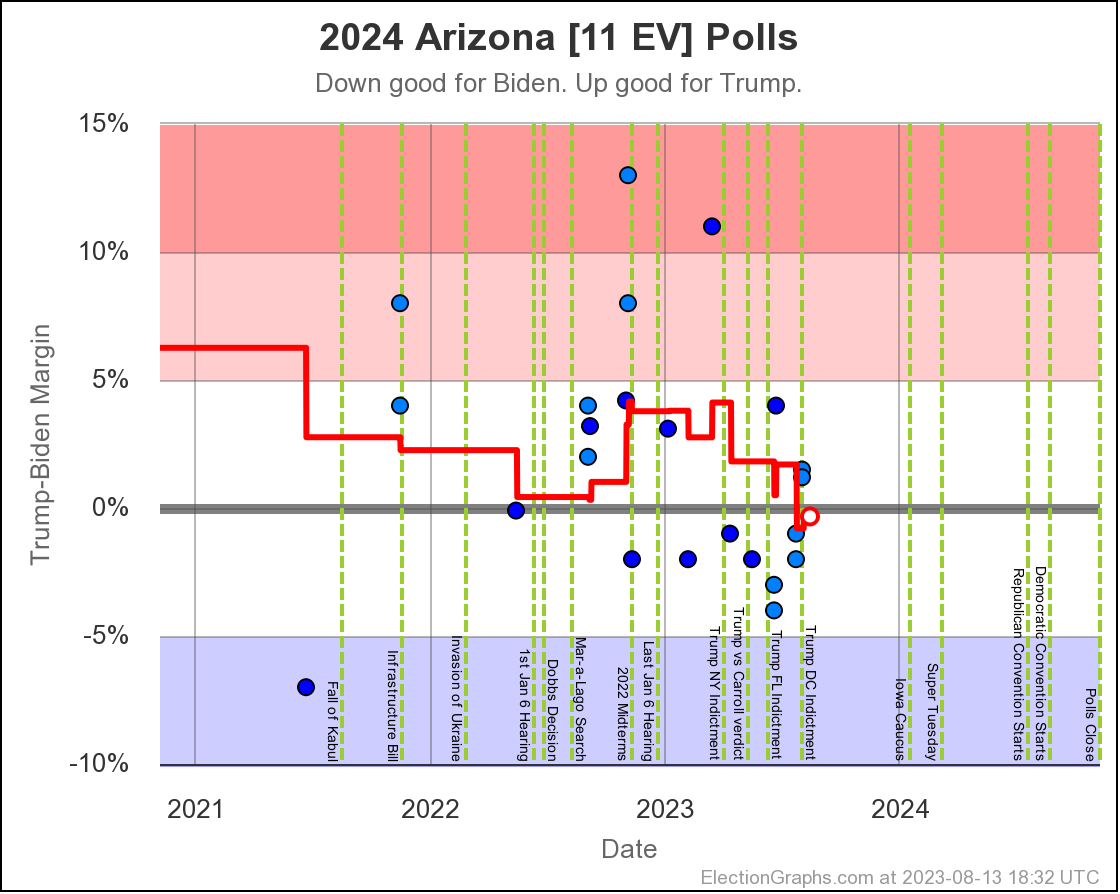
• Arizona (11 EV): Biden by 0.3% -> Trump by 0.3% (Trump+0.6%)
• Virginia (13 EV): Biden by 7.5% -> Biden by 7.0% (Trump+0.5%)
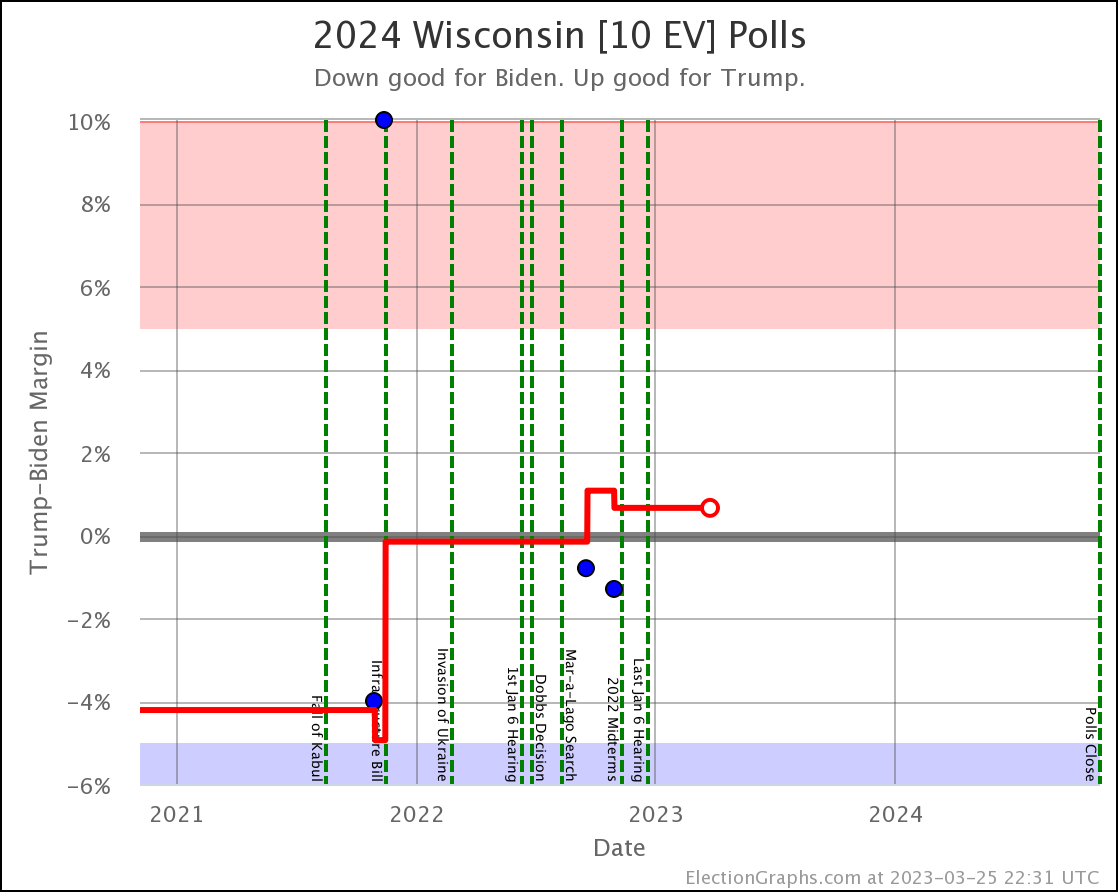
• Wisconsin (10 EV): Biden by 4.0% -> Biden by 3.8% (Trump+0.2%)
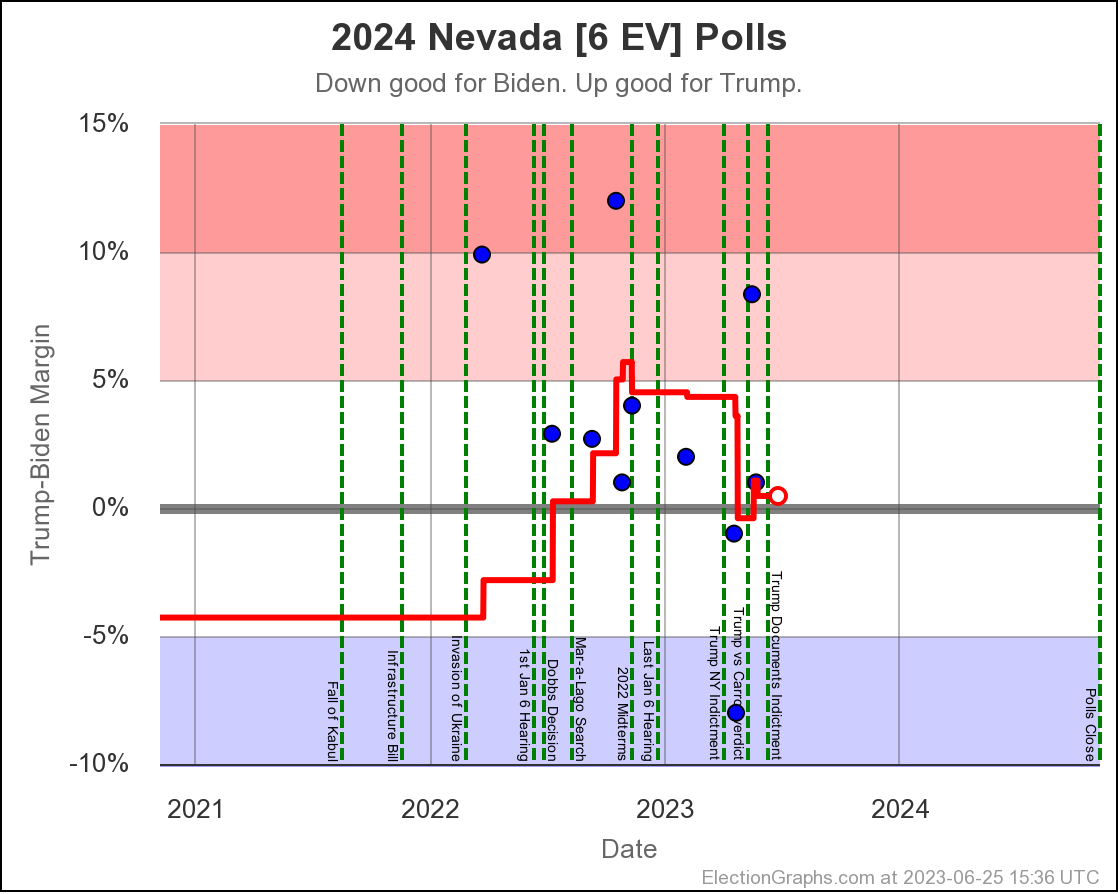
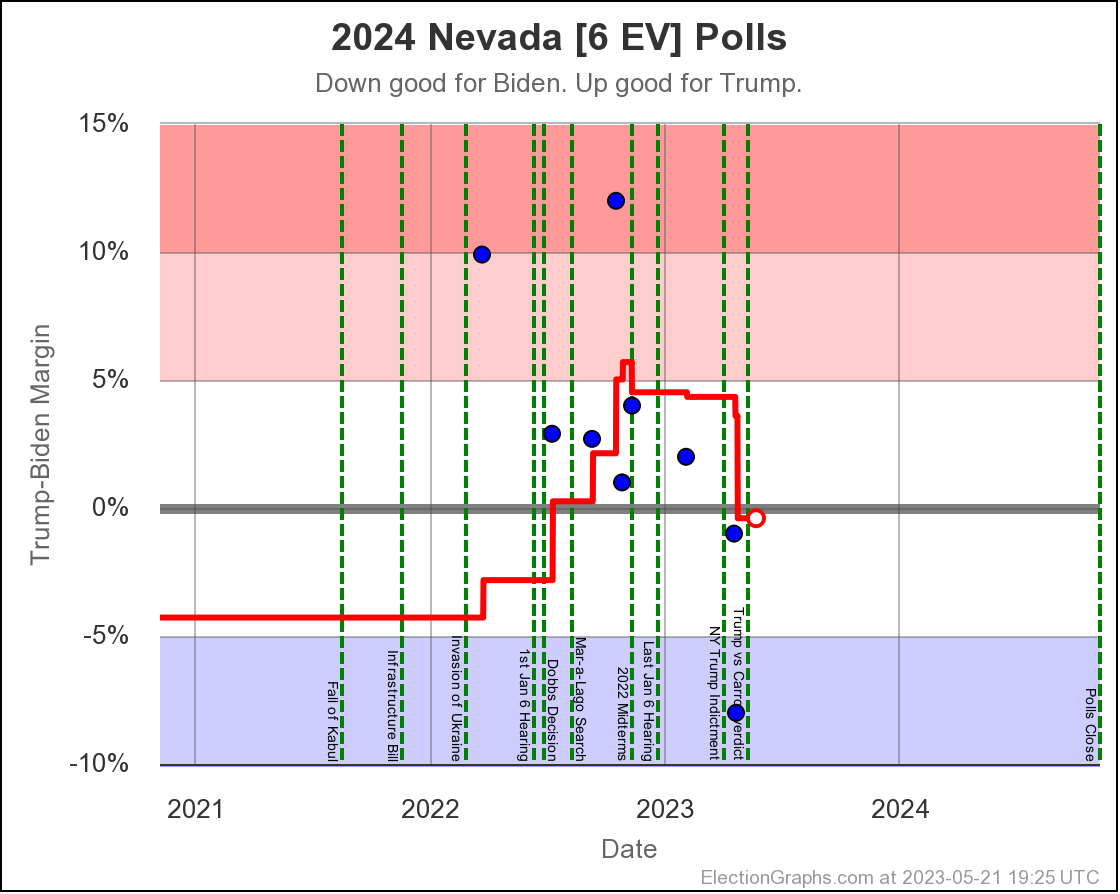
• Nevada (6 EV): Biden by 0.5% -> Biden by 0.3% (Trump+0.2%)
• Iowa (6 EV): Trump by 8.5% -> Trump by 8.6% (Trump+0.1%)

And the states where the poll average moved toward Biden are:

• Michigan (15 EV): Biden by 0.7% -> Biden by 2.0% (Biden+1.3%)
• North Carolina (16 EV): Trump by 2.6% -> Trump by 1.3% (Biden+1.3%)
• New Hampshire (4 EV): Biden by 6.0% -> Biden by 8.6% (Biden+2.6%)

Overall, this time more states in this center part of the spectrum are moving toward Trump than toward Biden.

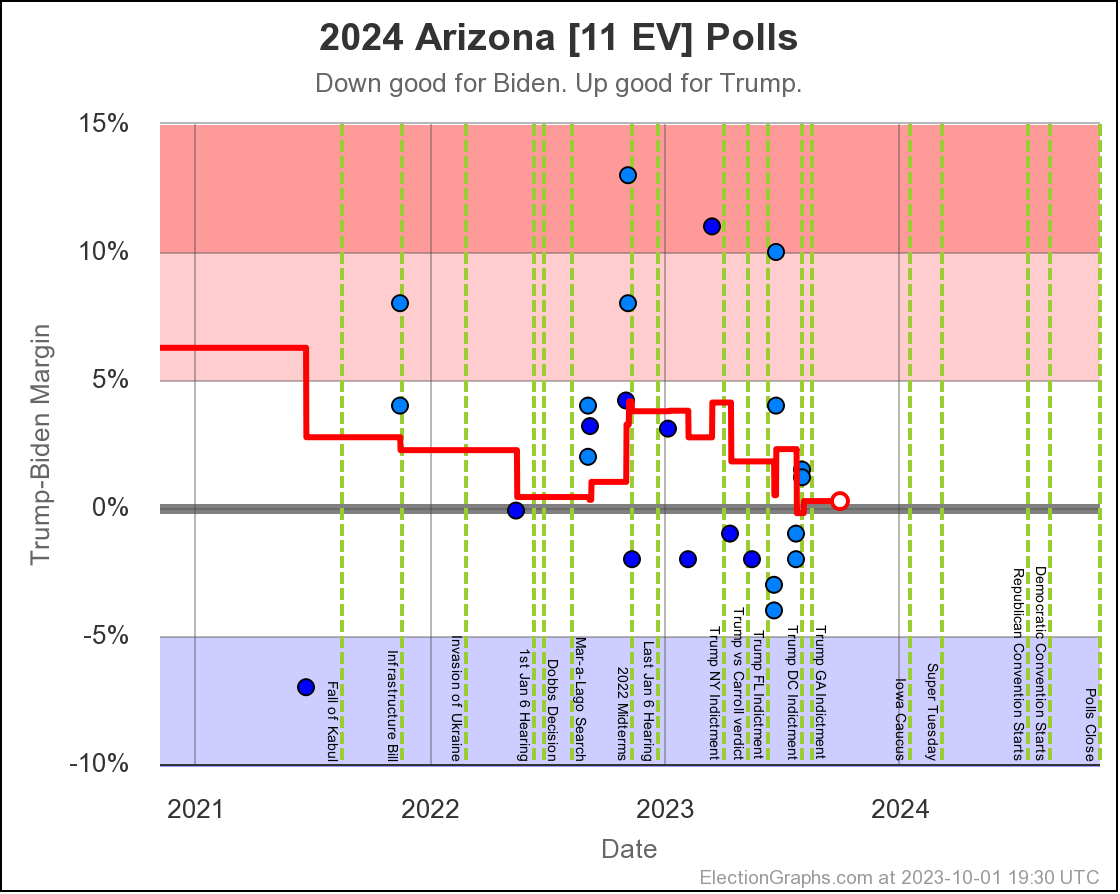
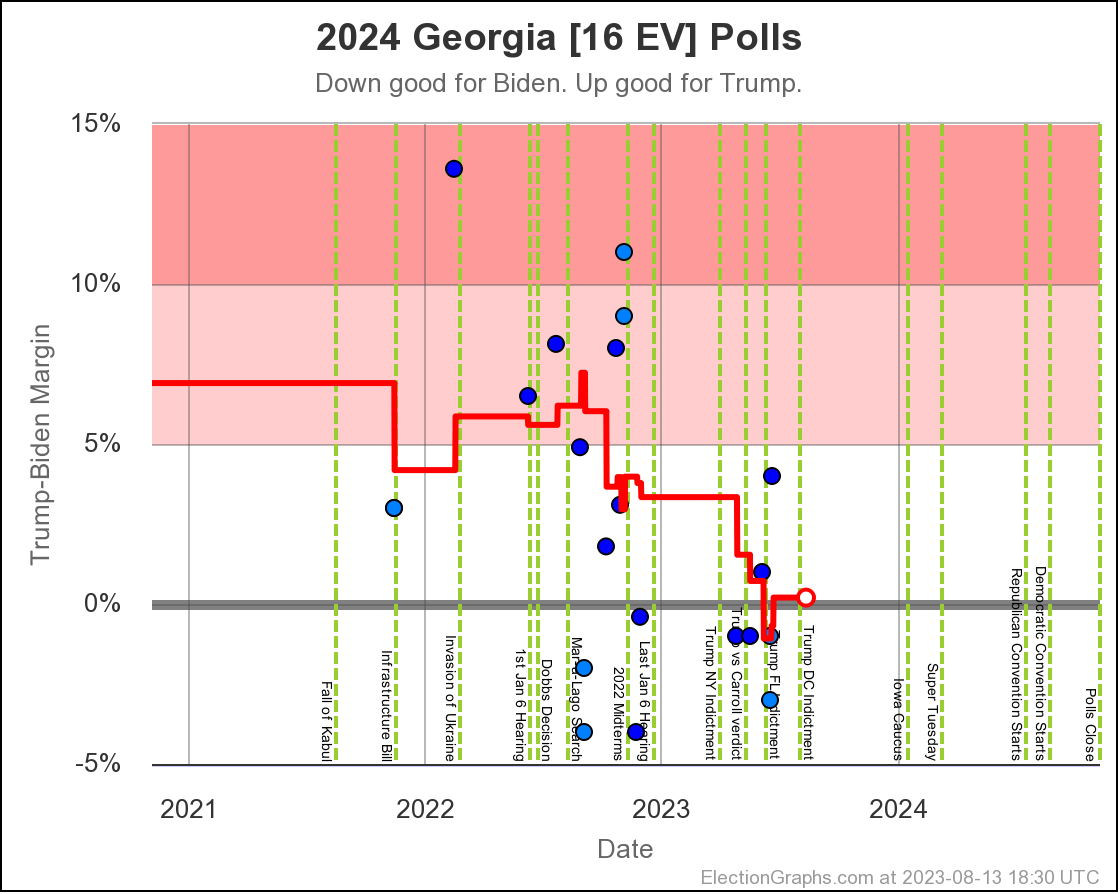
Only Arizona crossed the center line this time though. Lets see what is happening there:

Last time Arizona was just barely on the Biden side. Now it is just barely on the Trump side. All but one of the 5 polls in the average show a margin under 5%.

The exception is a Prime poll that released 2 results. First was a 4% Trump lead in a straight Biden vs Trump matchup. Second was if you added a hypothetical unnamed No Labels candidate. That expanded Trump's lead to 10%. In the case of polls that release multiple results, I include them as their average within the larger average, so this shows a 7% Trump lead for aggregate of the two Prime results. Absent that, Arizona would still be slightly on the blue side. But I don't pick and choose polls to include. The average is the average.

Given we are right on the edge, it would be reasonable to expect Arizona to bounce back and forth around that centerline a bit as the next few Arizona polls come in.

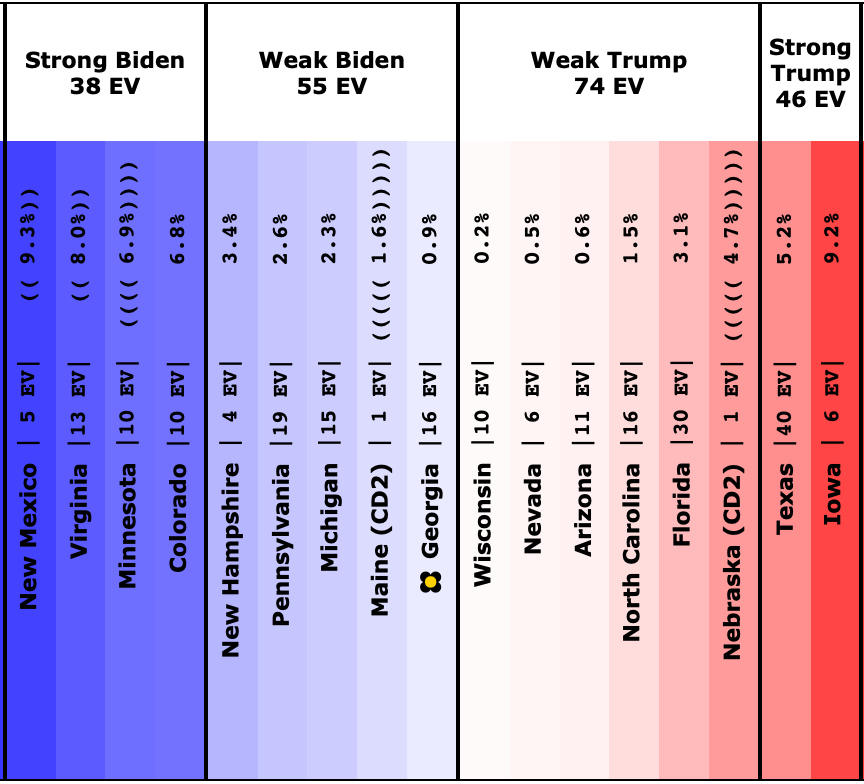
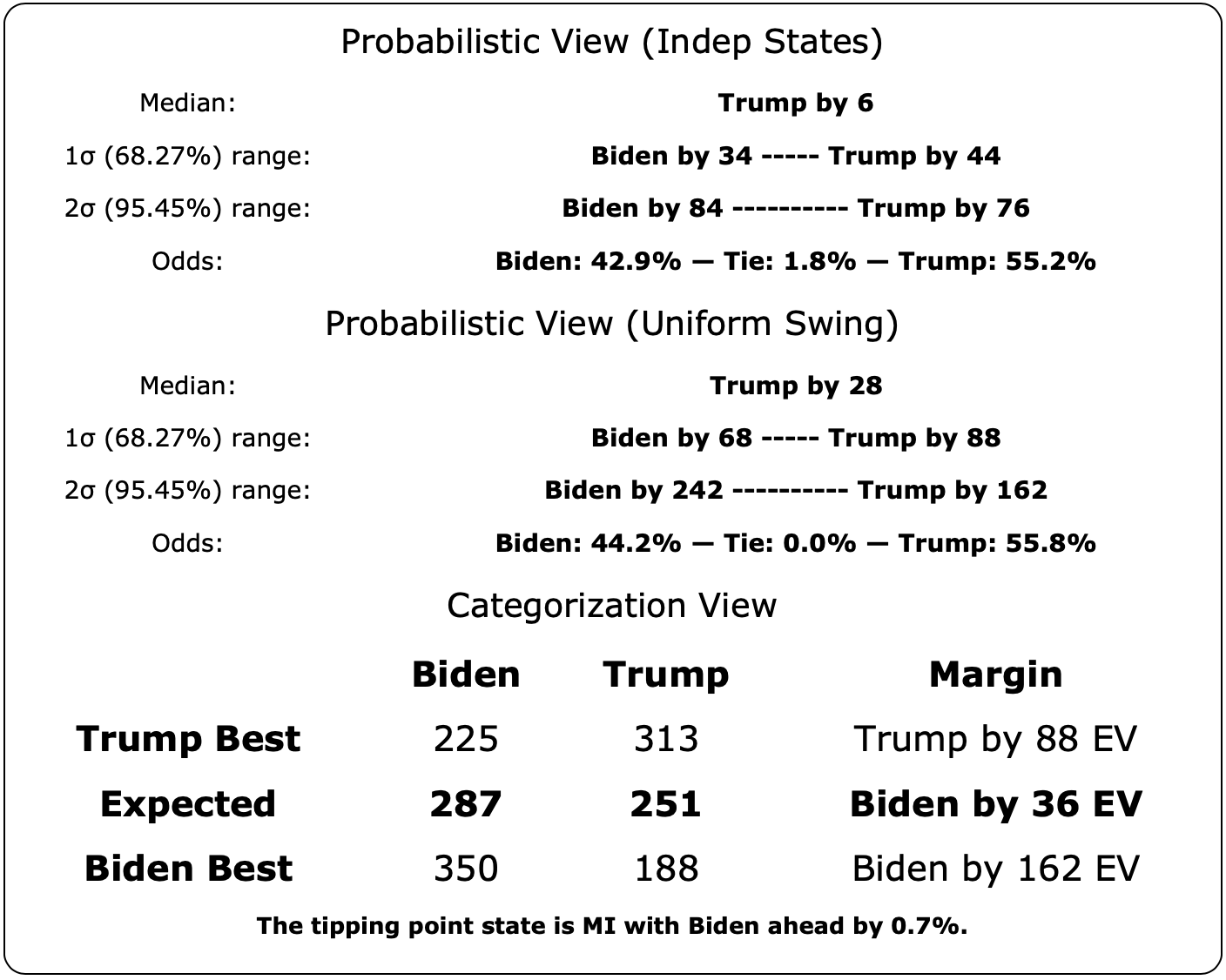
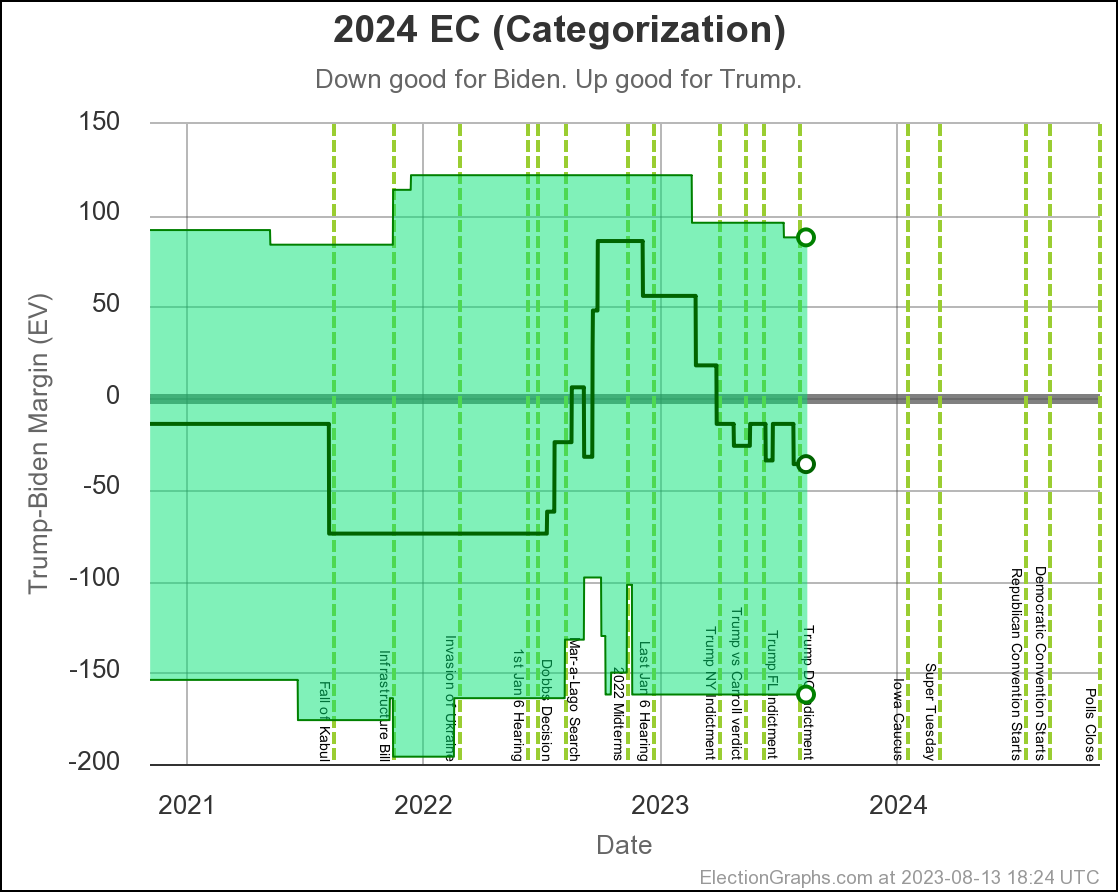
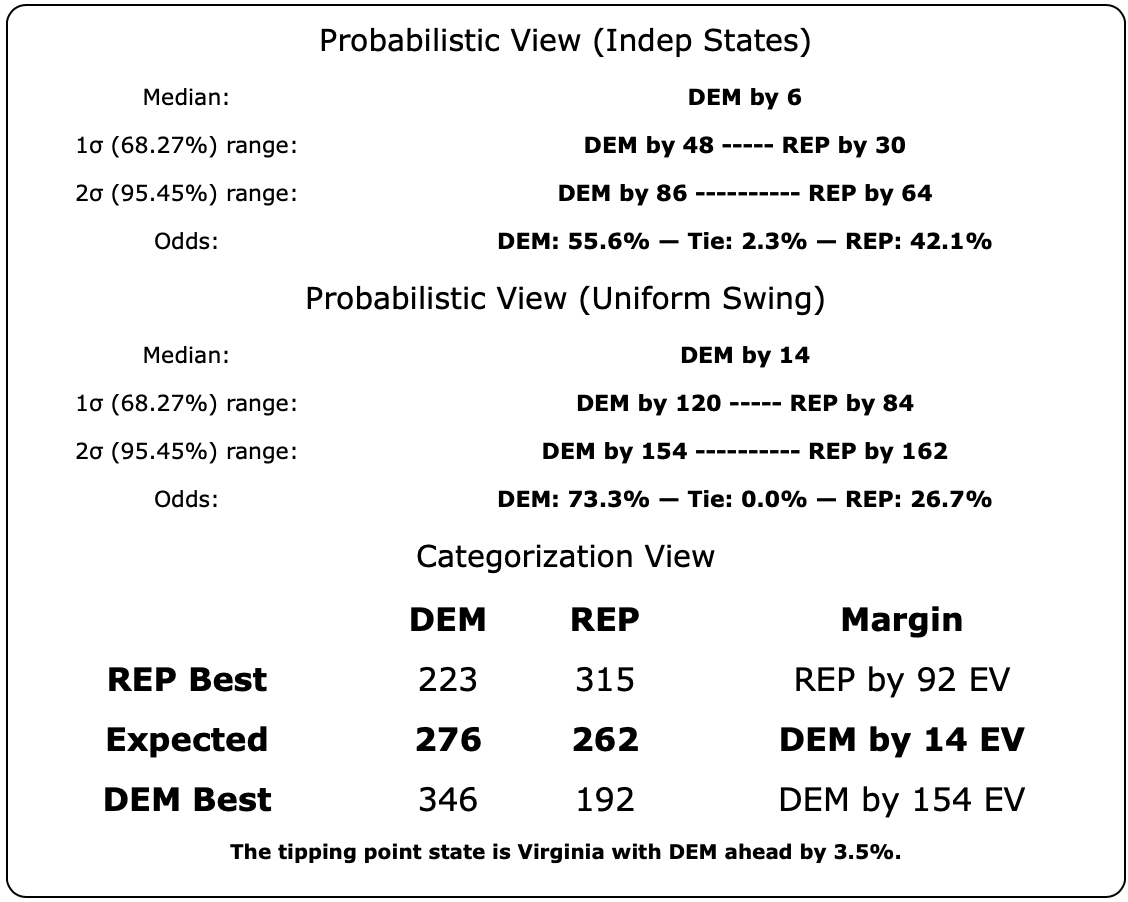
The same is true with all the "close states" really, although obviously some are closer to zero margin than others. They should all be considered states that could go either way, which is why in our summary, we show ranges of possibility, not point estimates. So here is what that looks like now:

Note that if you look at ANY of the ranges above, each looking at the situation in different ways, every single one of them includes either candidate winning. This is the nature of a close race.

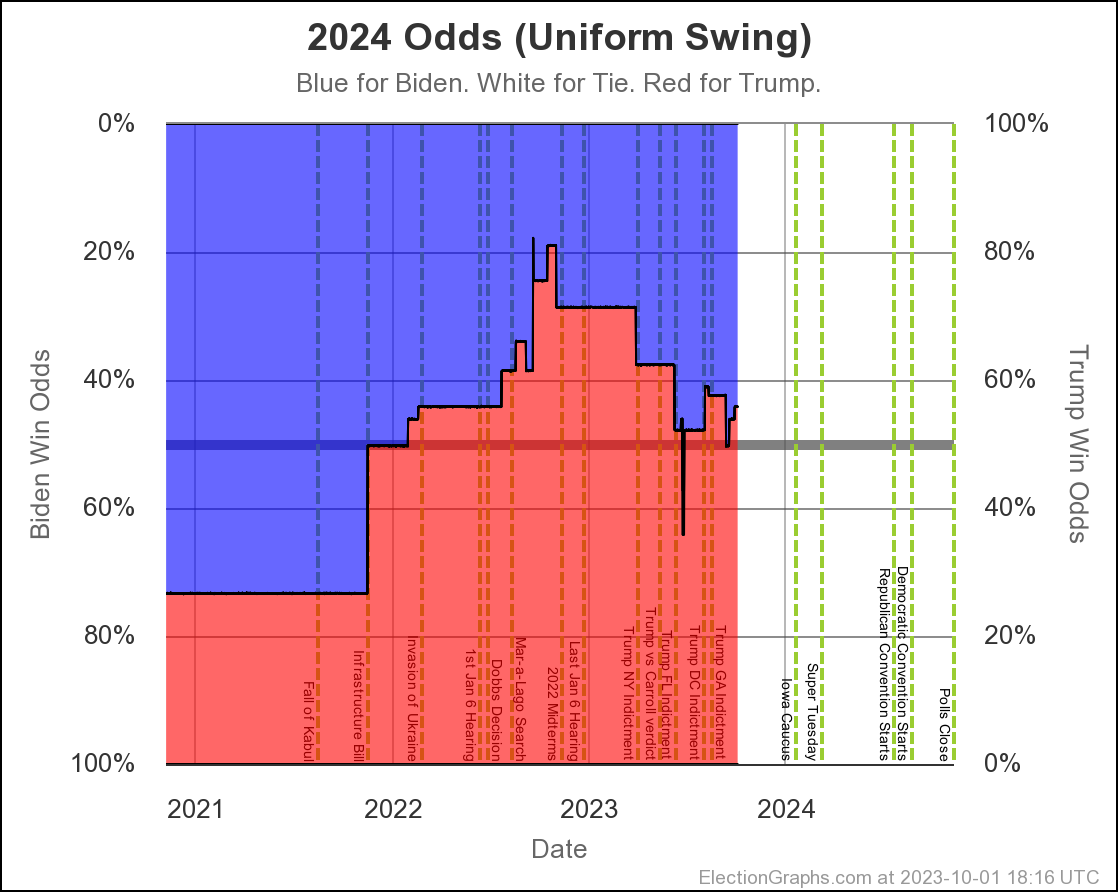
Both of my probabilistic views show Trump favored , while the straight up averages show Biden slightly favored. This is because the probabilistic views take into account that on average over the last four election cycles, the polls have underestimated the Republican in the closest states. But either way, they all show a race that could go either way.

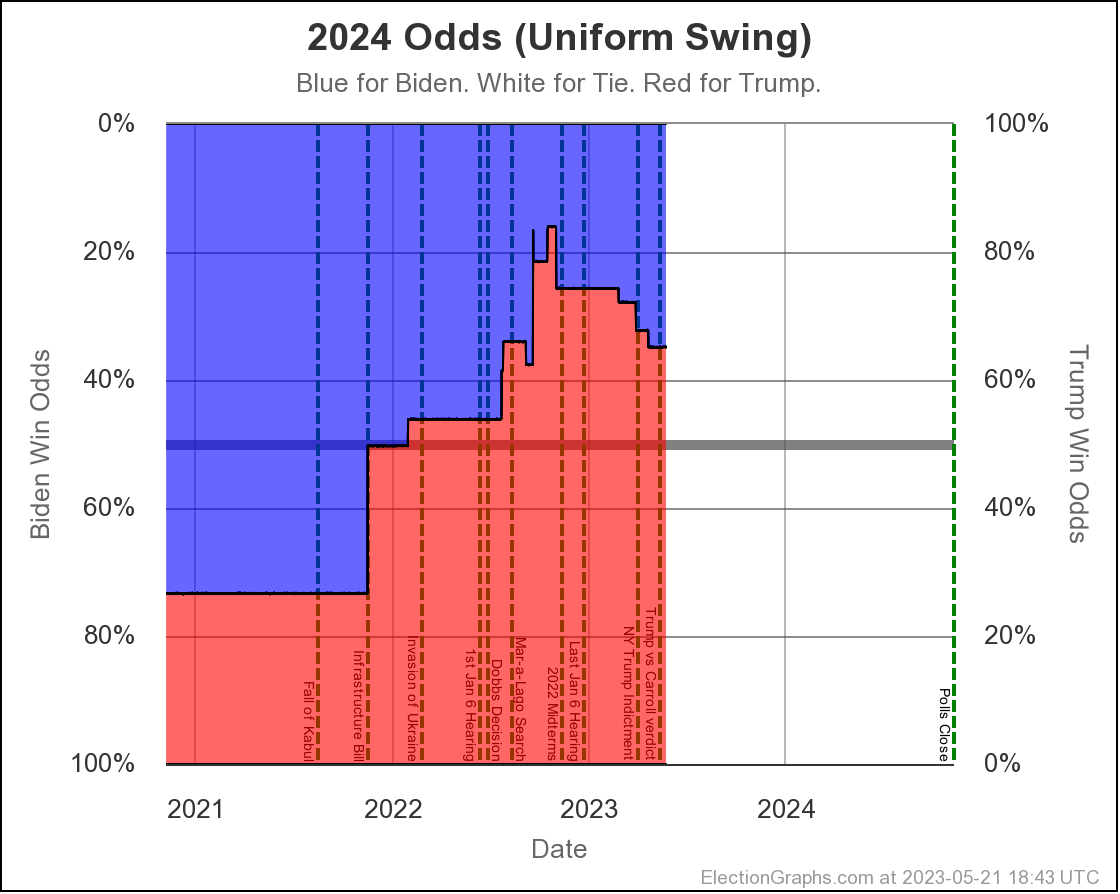
Lets look at the evolution of the Biden win odds in these blog post updates:

• 2023-03-25: Between 17.8% and 25.8%
• 2023-04-24: Between 24.9% and 32.3%
• 2023-05-21: Between 34.9% and 35.9%
• 2023-06-25: Between 43.9% and 46.0%
• 2023-08-13: Between 42.9% and 44.2%
• 2023-10-01: Between 35.7% and 44.2%

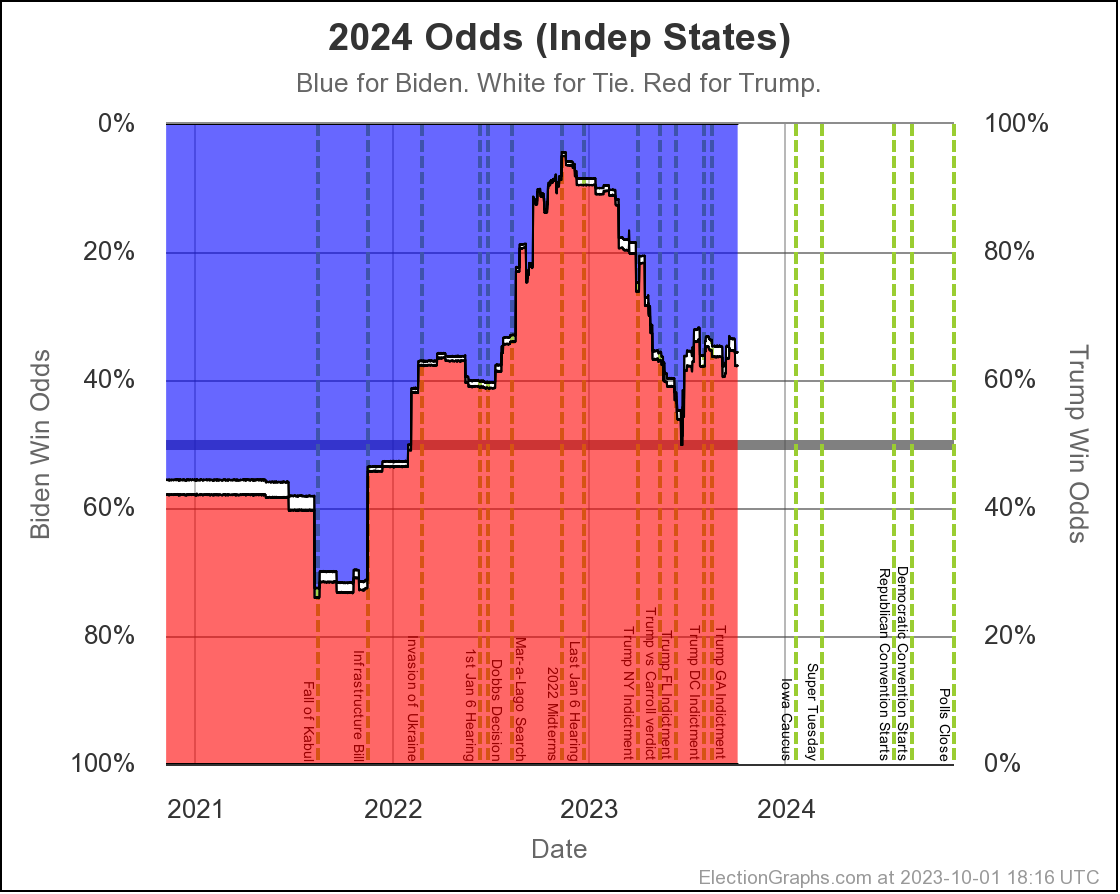
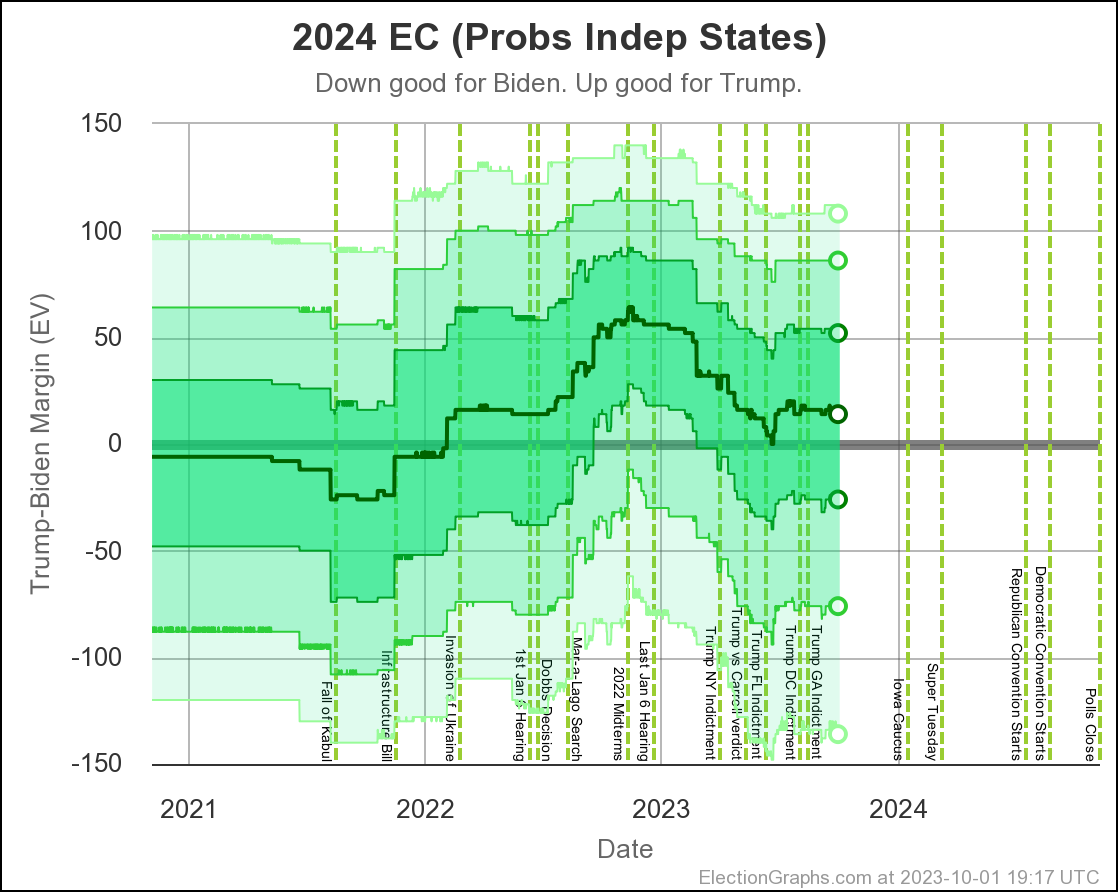
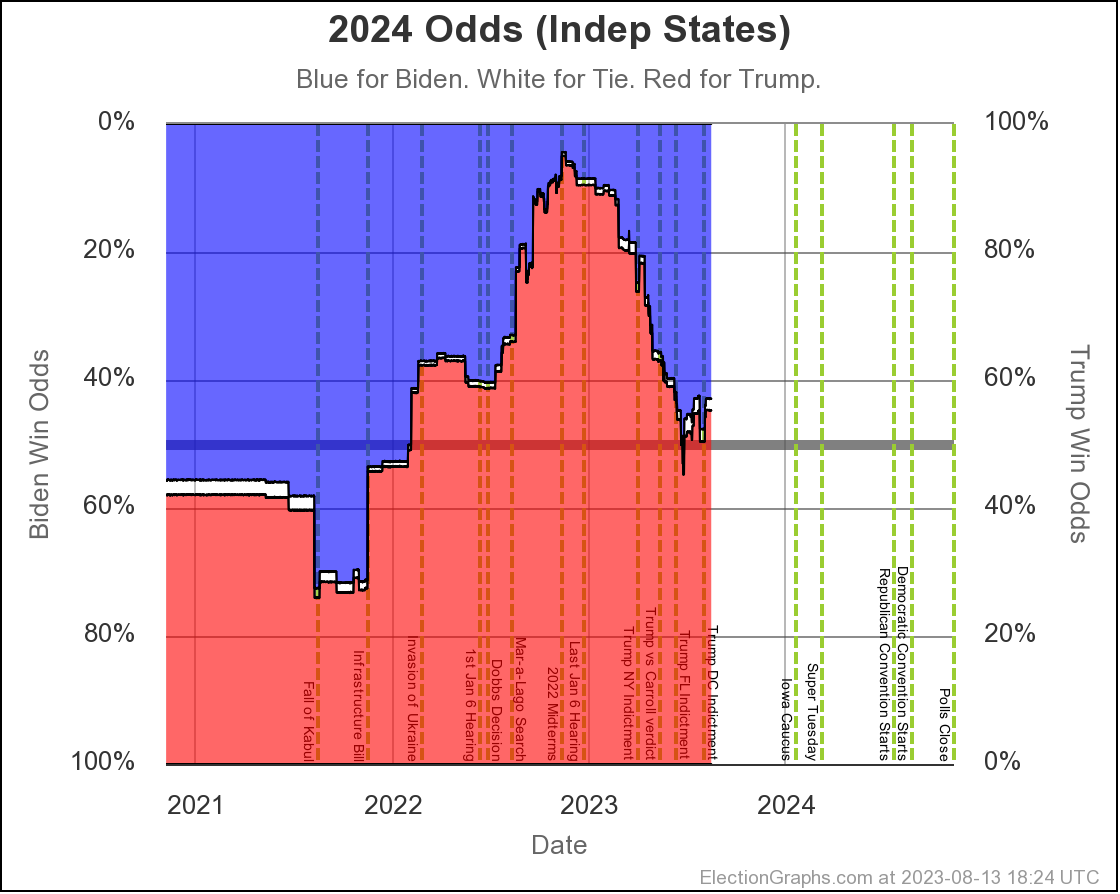
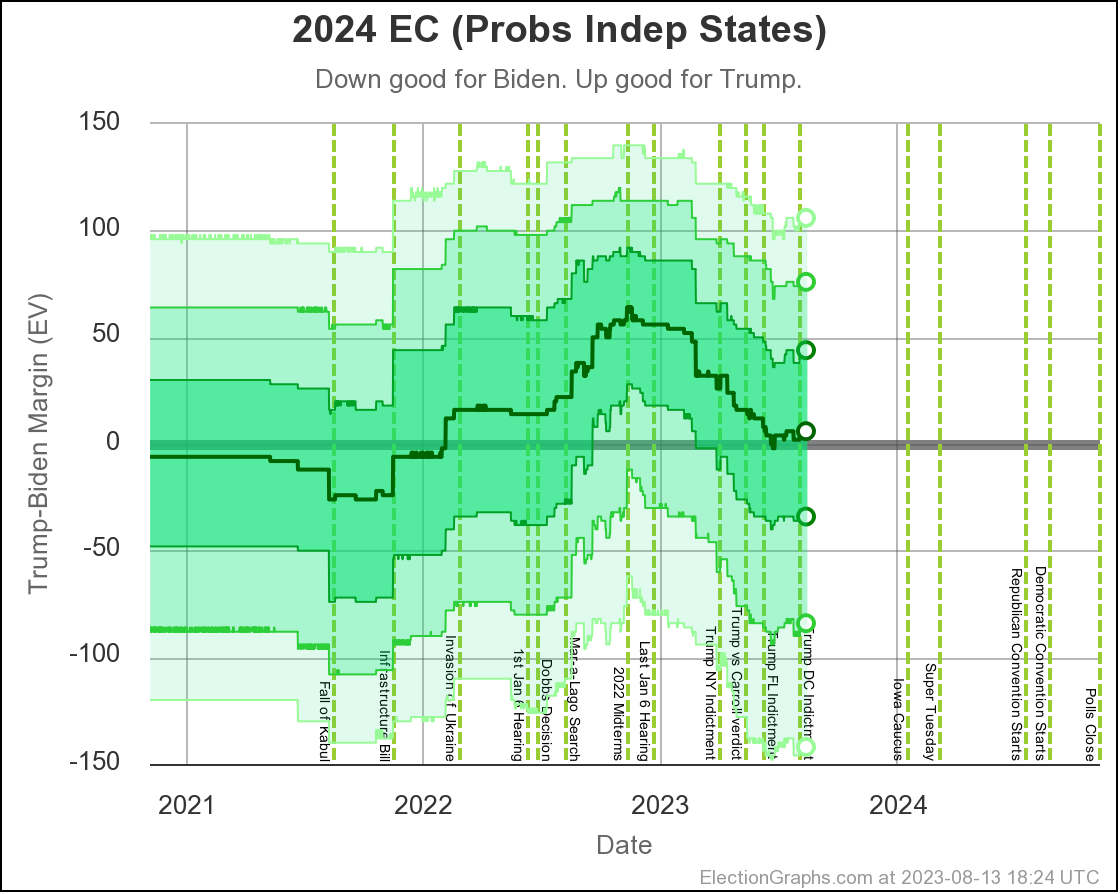
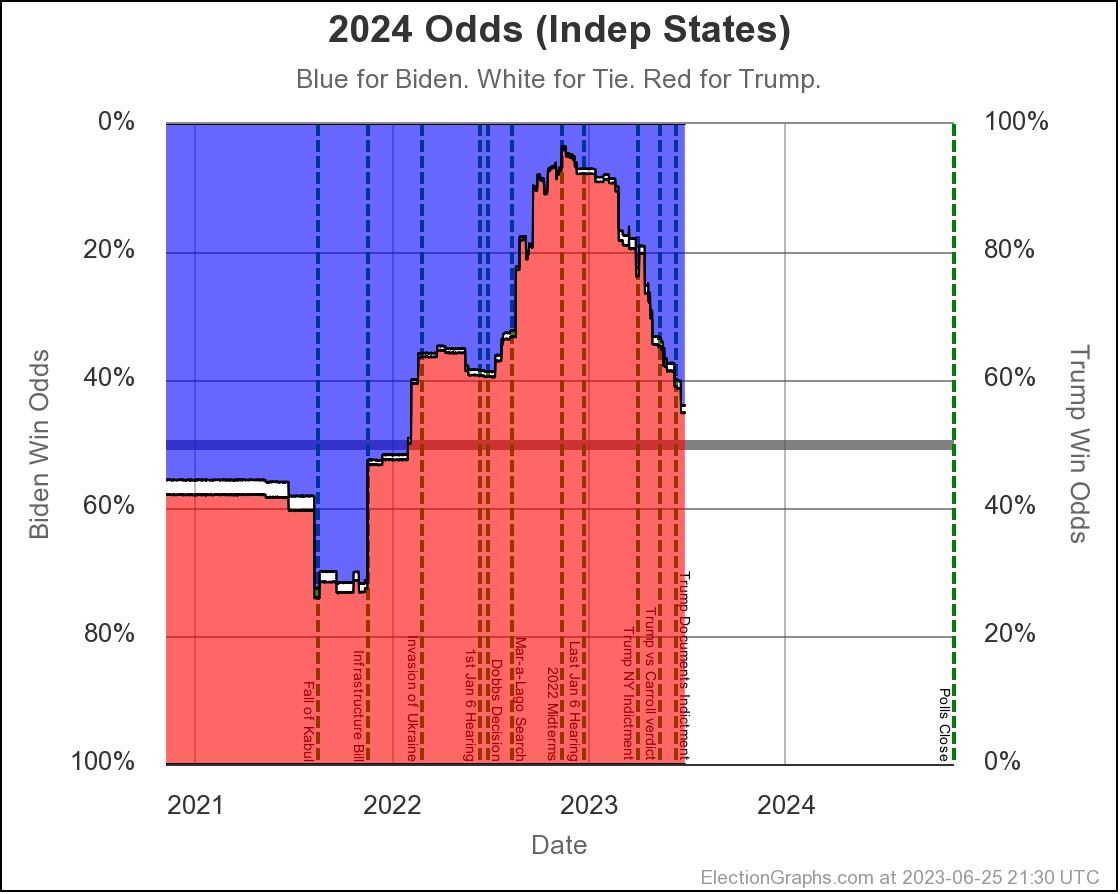
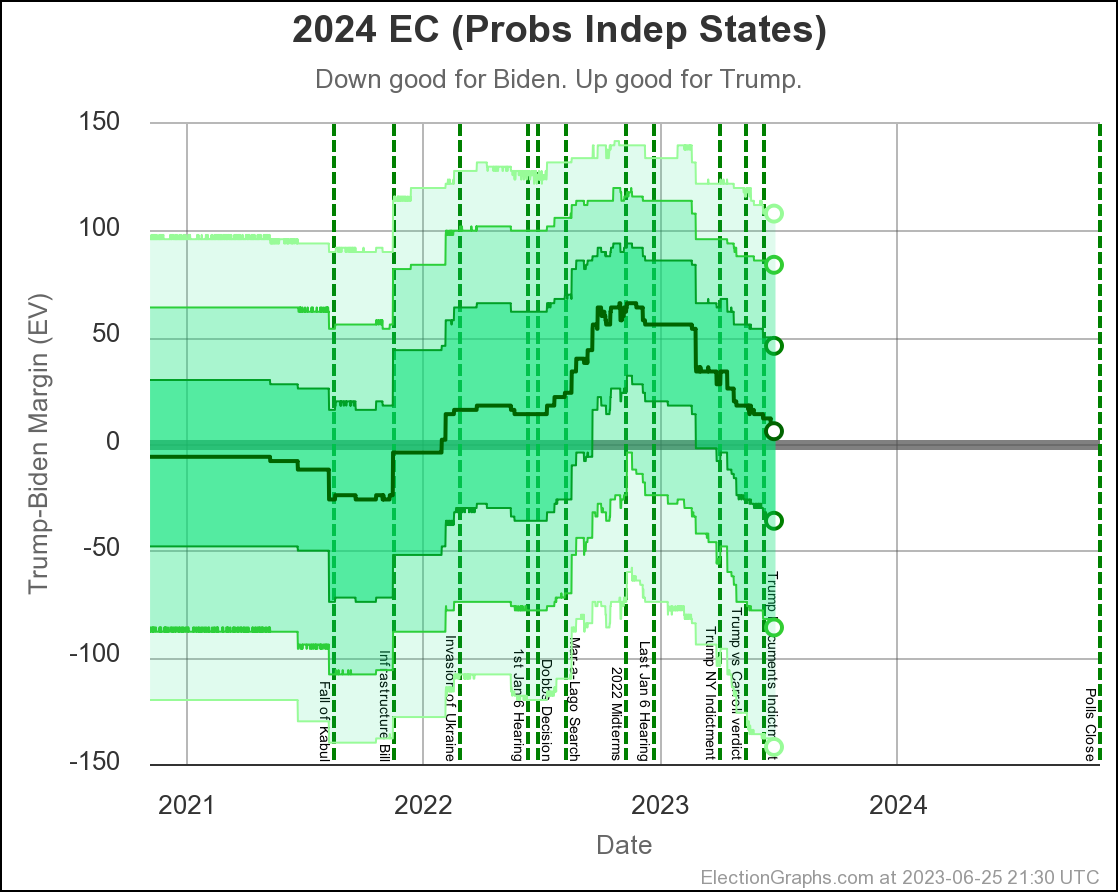
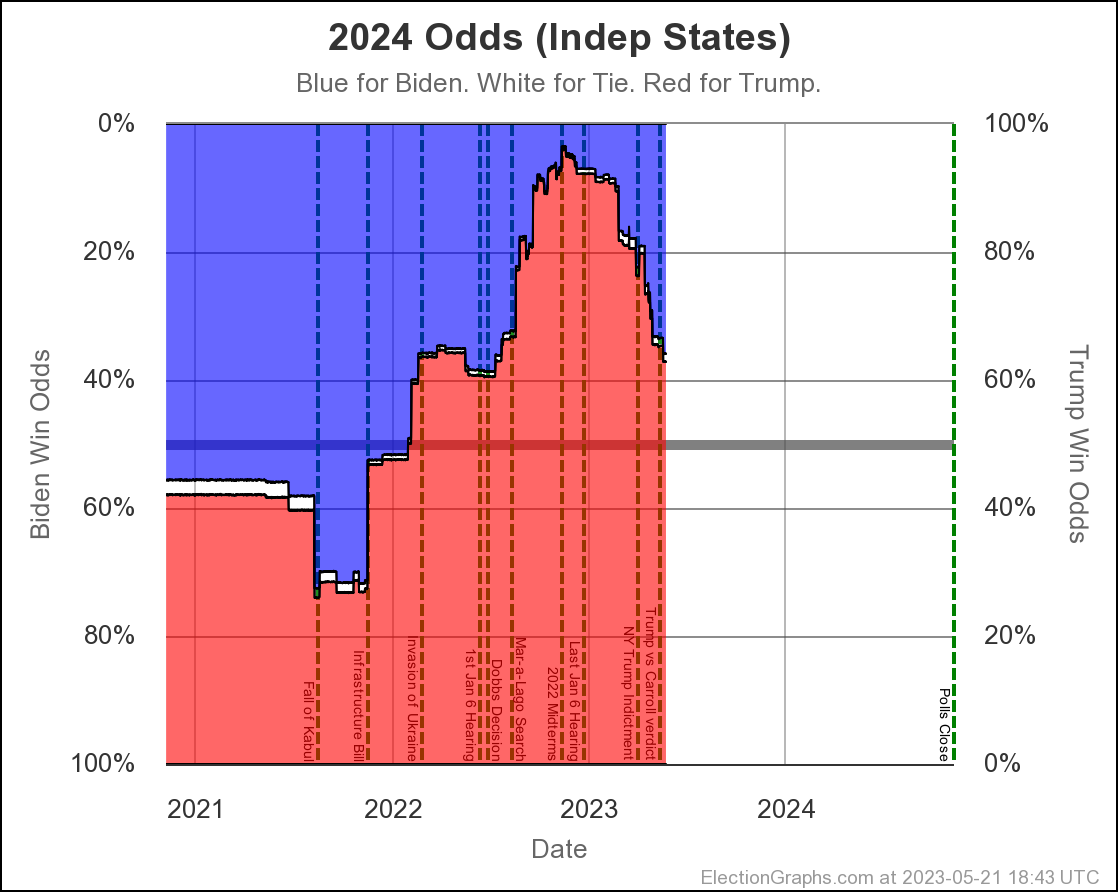
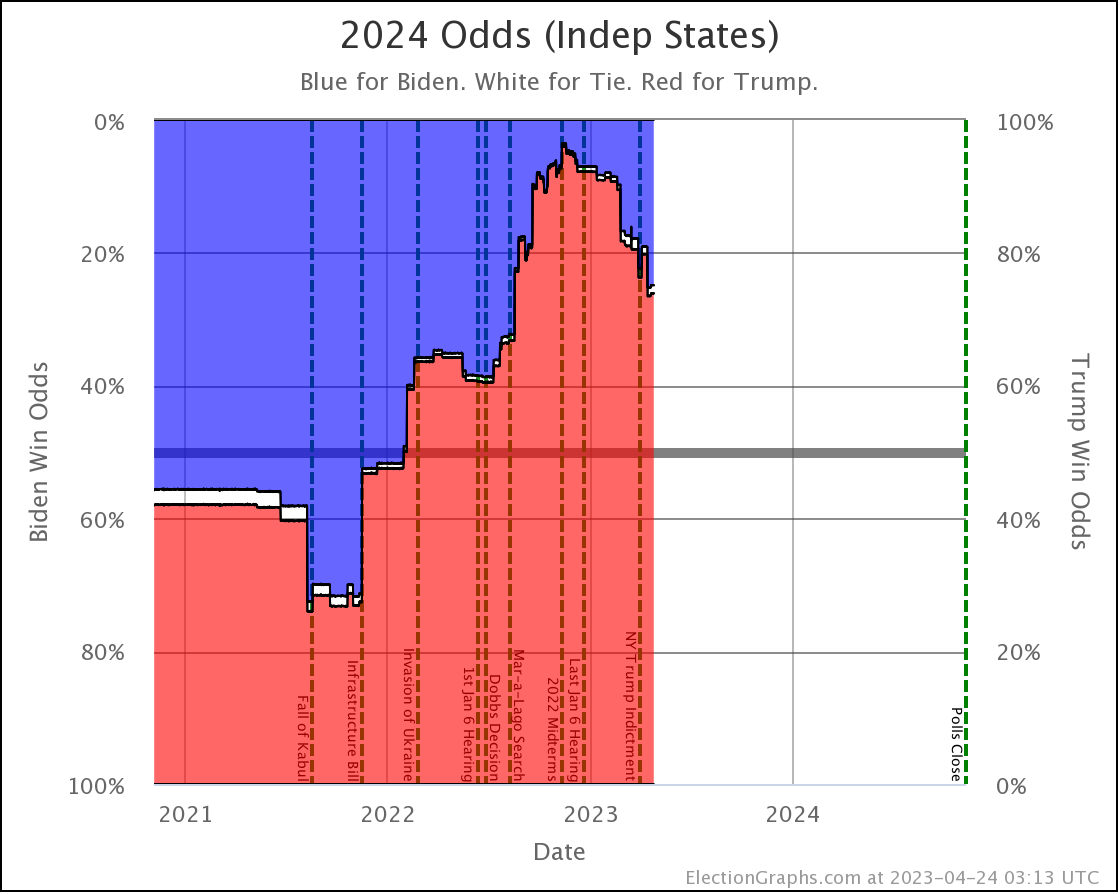
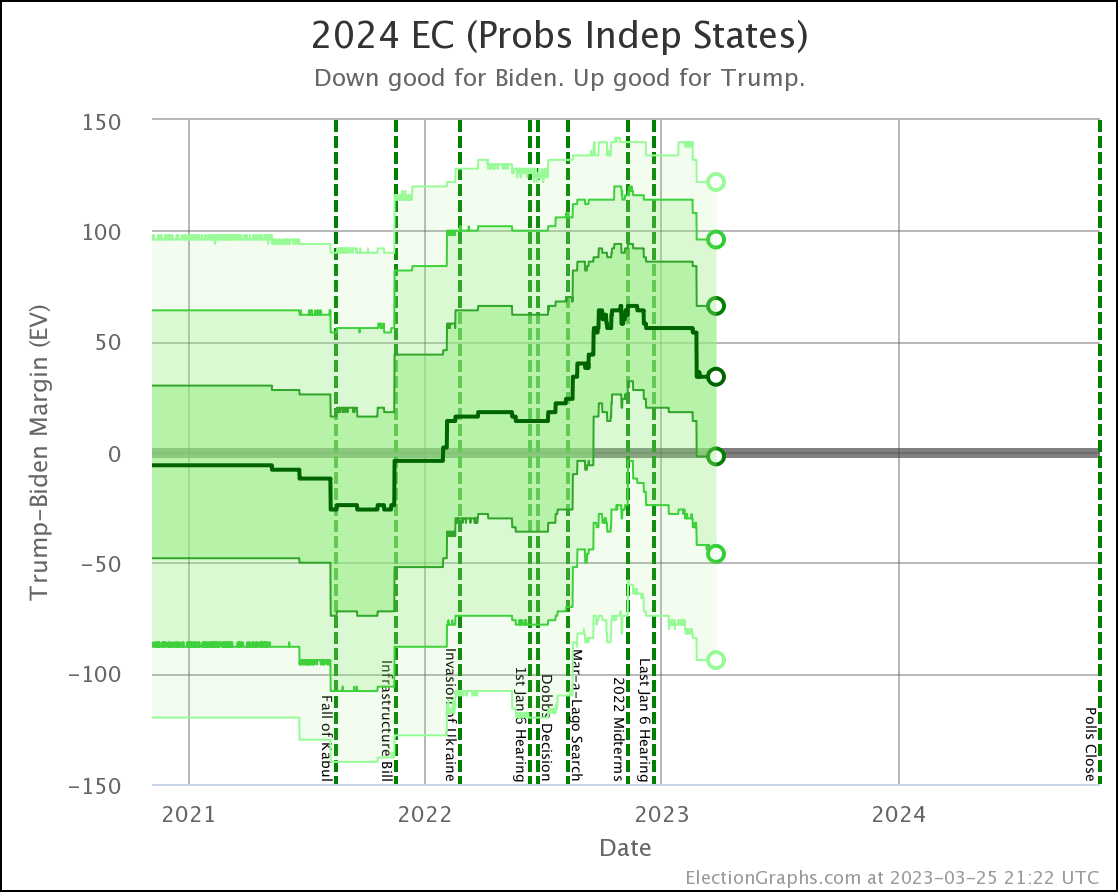
The net result of all the state level changes definitely puts Biden in a weaker position than at the last update. Lets look at the "Independent States" chart first, since it is the most dynamic:

Where are we? Well, you can see that things were generally heading toward Biden from November 2022 until the end of June 2023, then things popped back up toward Trump a bit, and things have actually been pretty stable since then.

But wait, it popped back toward Trump at the end of June?

But the last update was in August I can hear you saying.

Yes. But remember that Prime poll in Arizona? The one with the No Labels alternative result? I had initially entered that data into the Election Graphs system with only the straight Biden vs Trump result when it came out in June. Sometime later I determined that I had made a mistake in not entering these secondary results on a whole bunch of polls, and went through a process over several weeks of fixing that.

Prime had released polls in Arizona, Georgia, Michigan, North Carolina, Nevada, Pennsylvania, and Wisconsin. All close states. These had generally been favorable to Trump anyway, and there already was a bit of a pop back in the Trump direction showing when I did the August update, but their results with the hypothetical No Labels candidate showed the 3P candidate helping Trump in every one of those states except North Carolina (where there was no impact).

On average in the Prime polls in those 7 states, the presence of a No Labels candidate helped Trump (and hurt Biden) by a net change of 4.3% on the margin.

So when I folded in the Prime data including No Labels in August, since these results were all good for Trump in a whole bunch of close states, it moved all the curves in the Trump direction from June through the present.

And we have been pretty stable since then. When these polls roll off the averages as new polls come in, if the new polls don't show the same impact, things will move back in Biden's direction a bit.

Of course, most other polls do not include a No Labels contender. If we actually end up with a No Labels candidate, these polls that included them may end up being the ones that are closer to right.

Once various possible 3P candidates become "real" rather than just hypothetical more polling outfits will include them. 3P candidates also usually fade as the election approaches though.

We shall see.

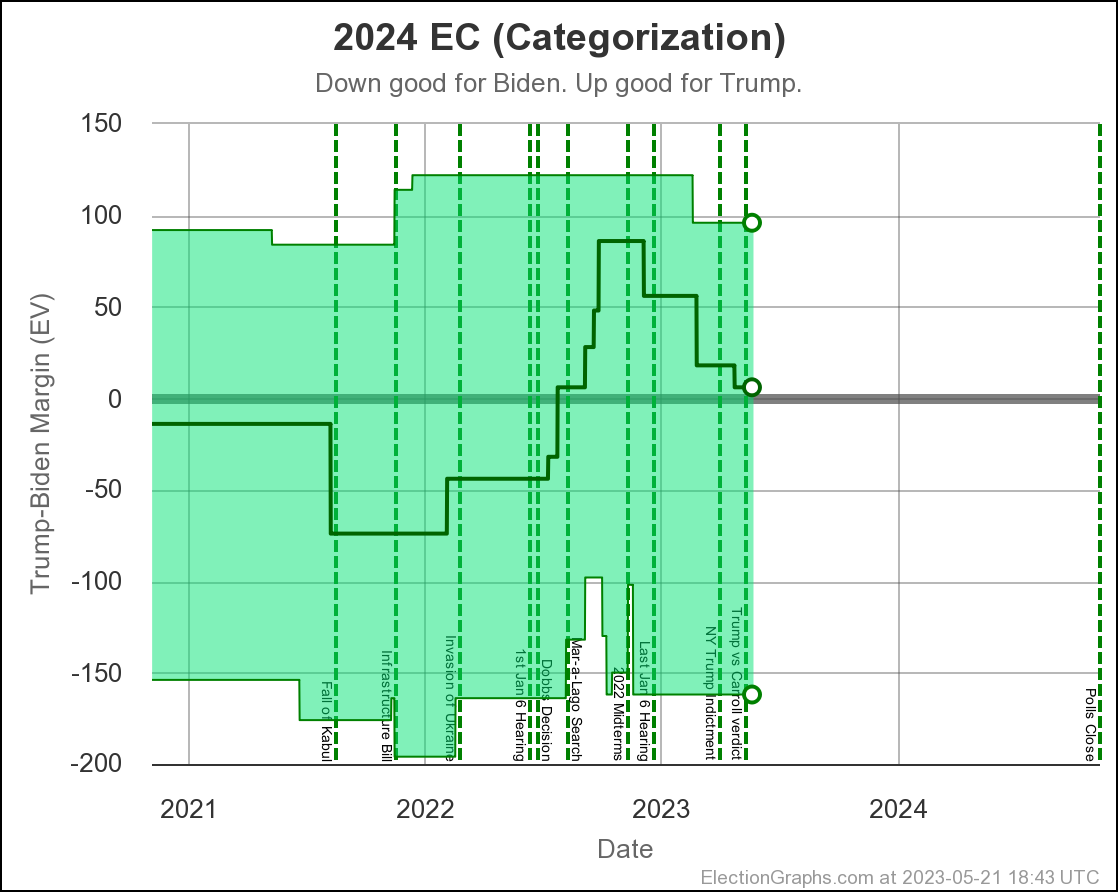
In terms of the actual Electoral College margin predicted by the Independent States view, the chart looks like this:

The tie line is well within the darkest band, which is the 1σ (68.27%) band. Every view shows a close race, so we should not be surprised.

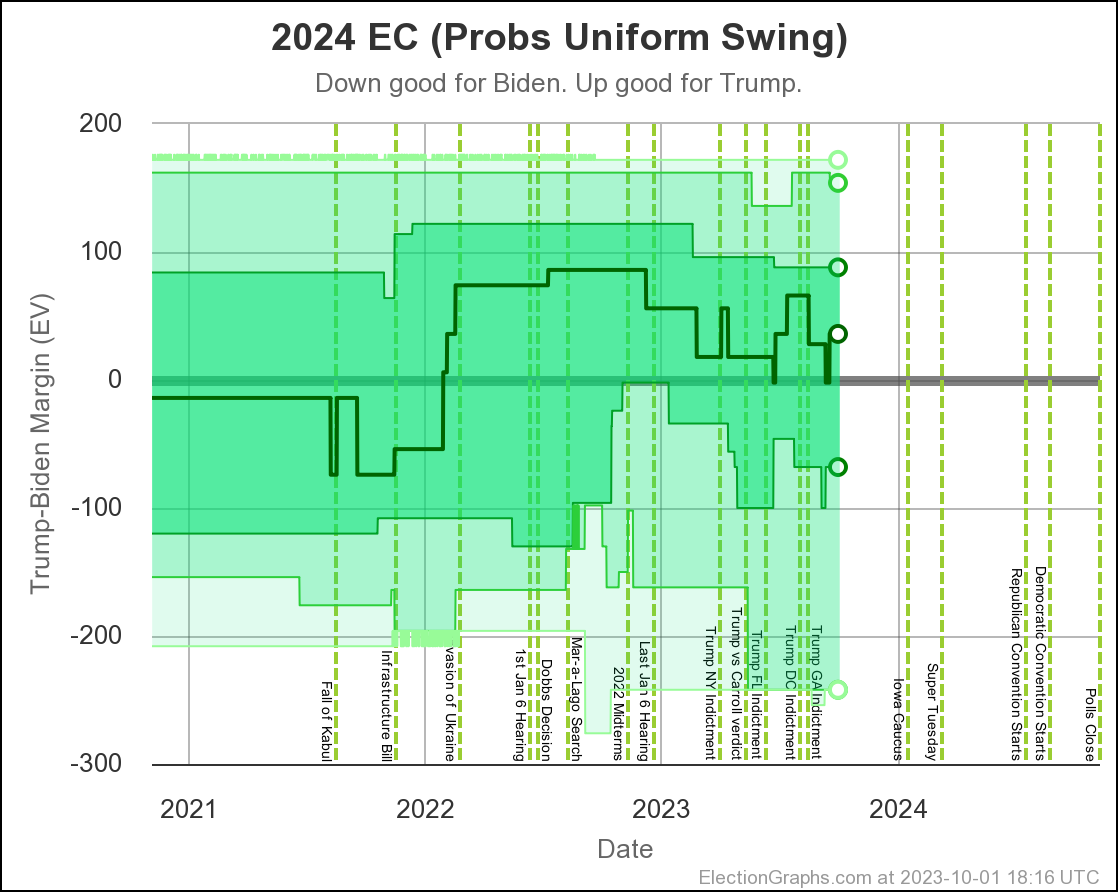
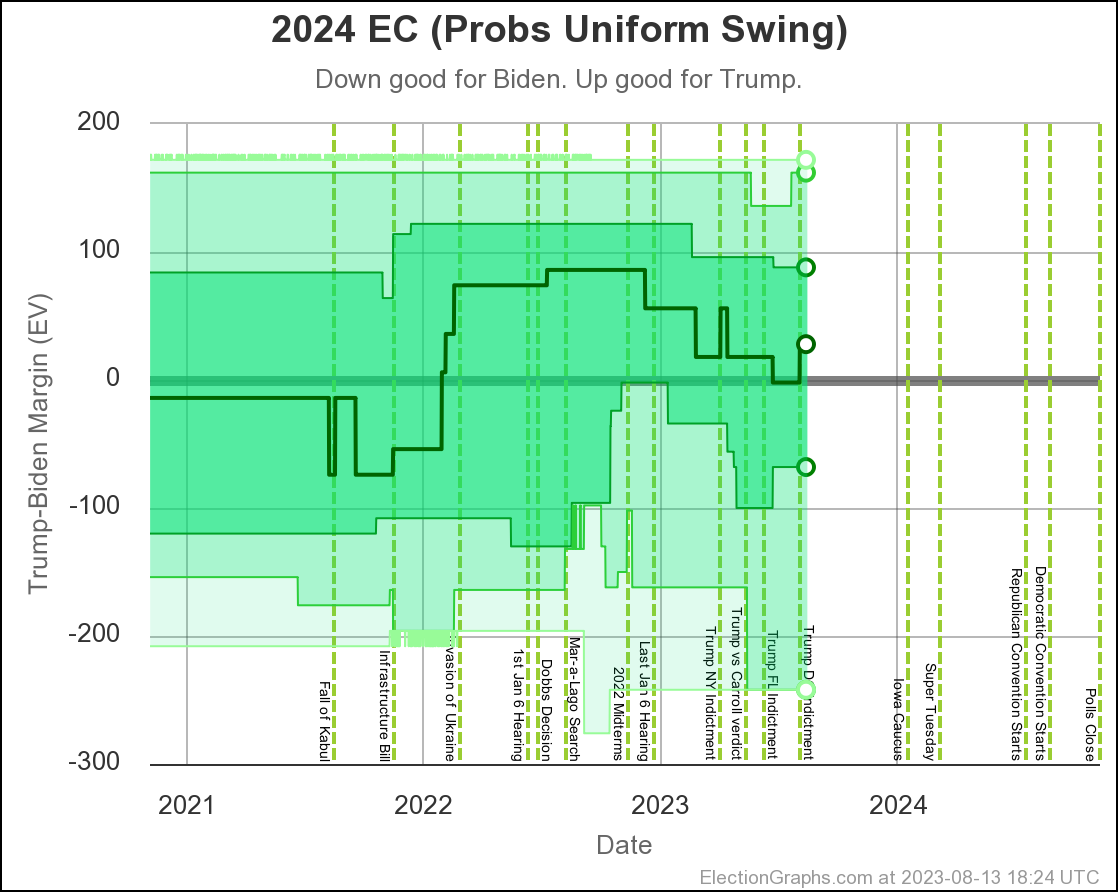
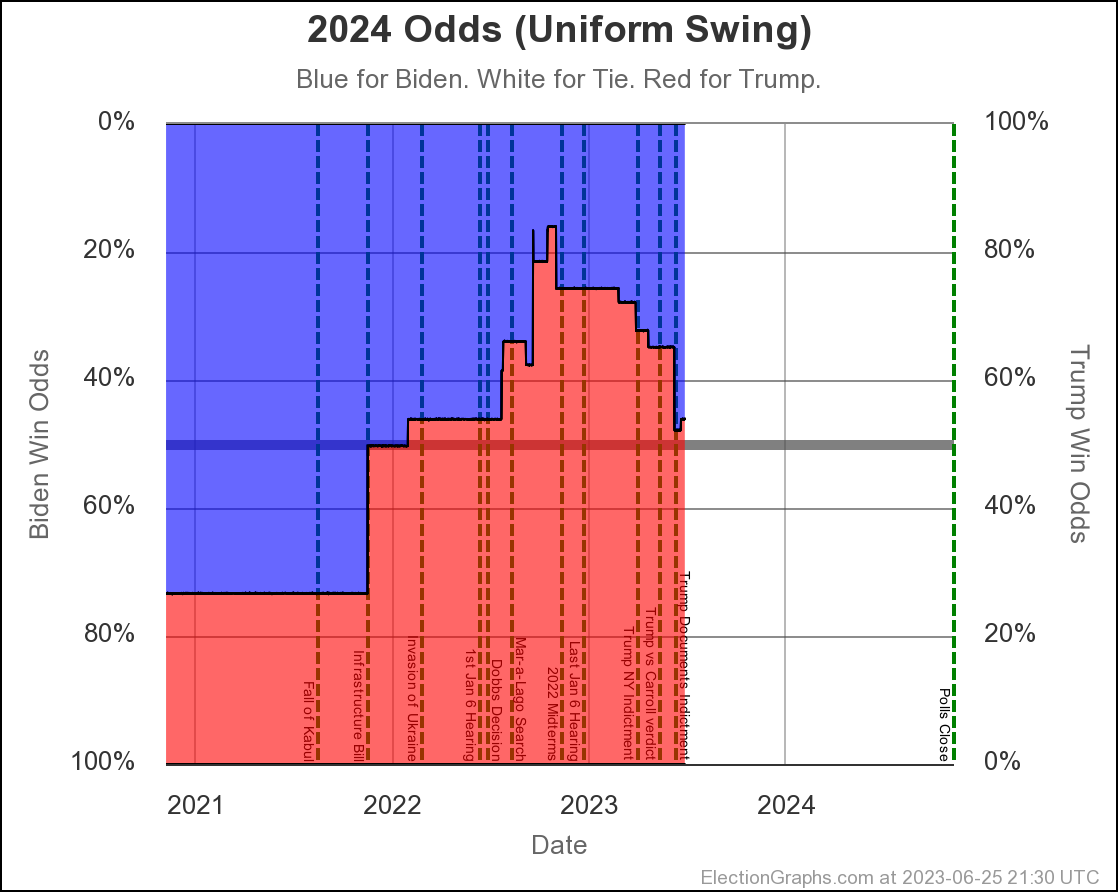
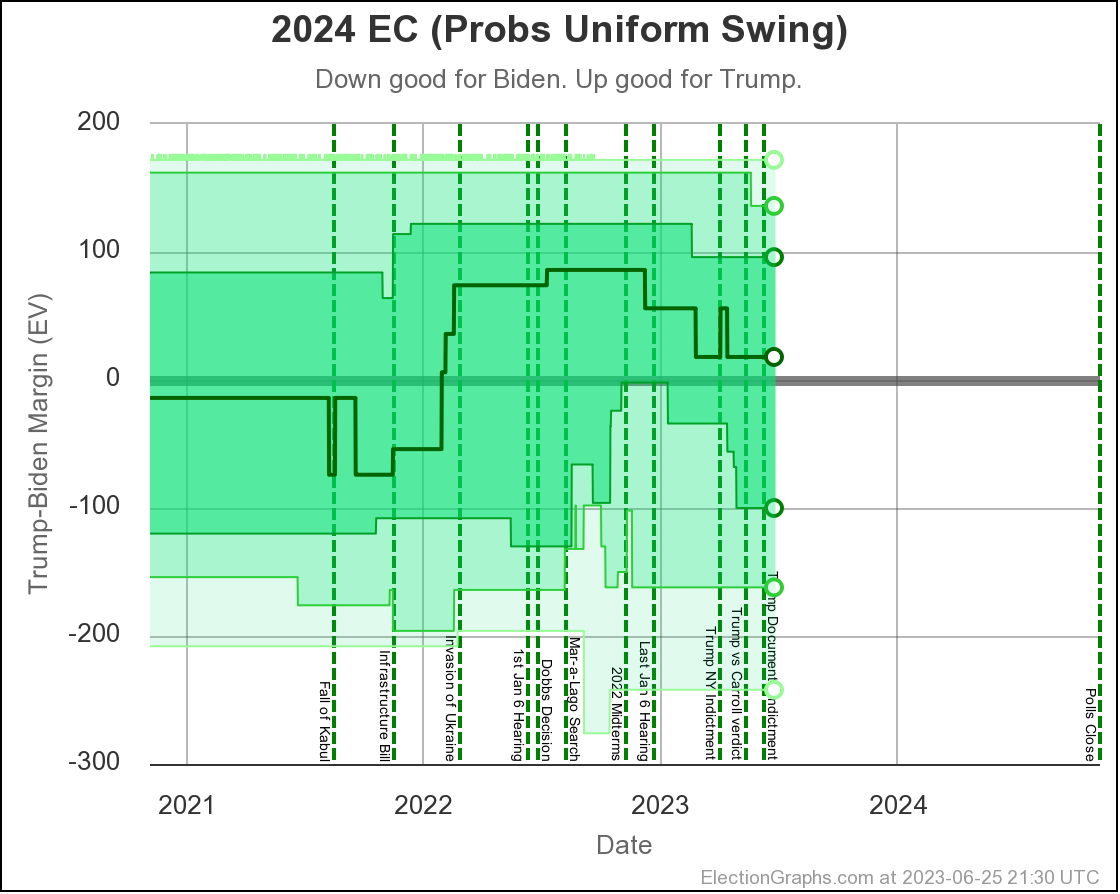
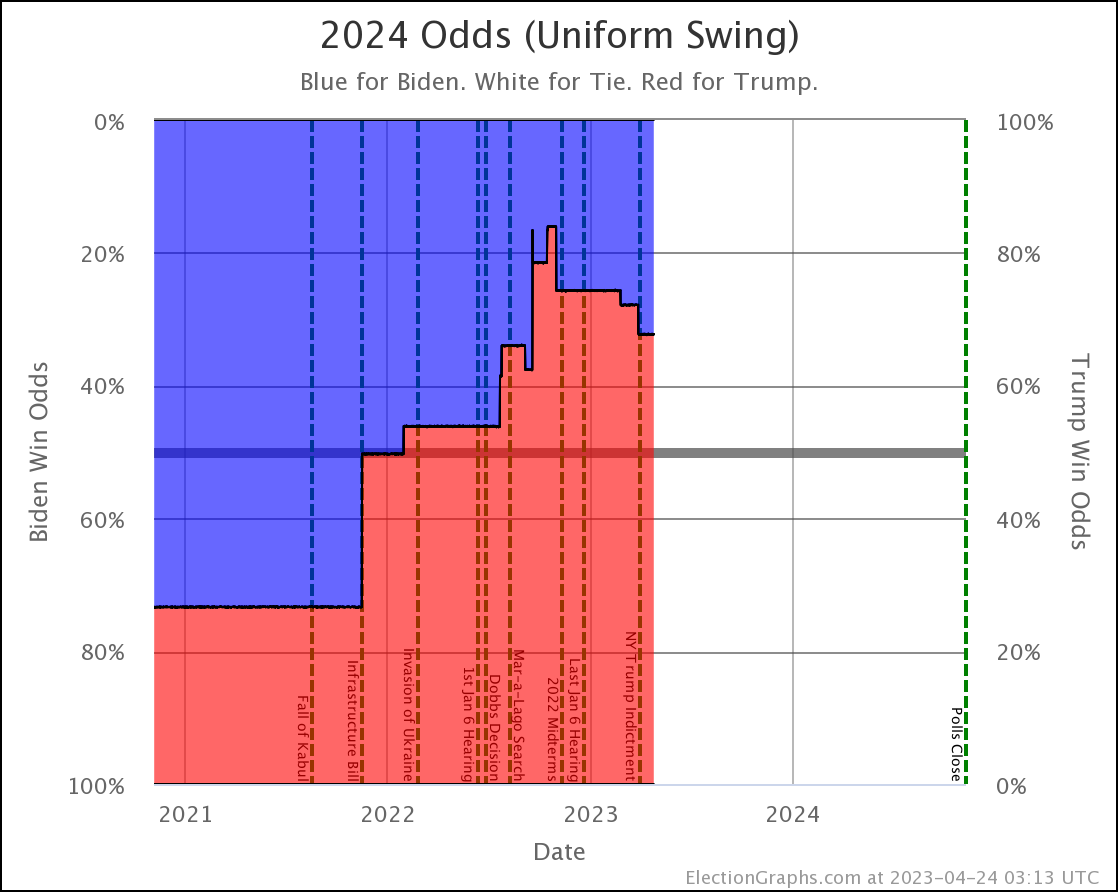
The two Uniform Swing views look similar, but with a wider range of outcomes and a "blockier" appearance:

Just looking at straight poll averages, and considering any margin less than 5% too close to call, the midpoint has moved around a bit, but the overall range of possibilities hasn't changed all that much.

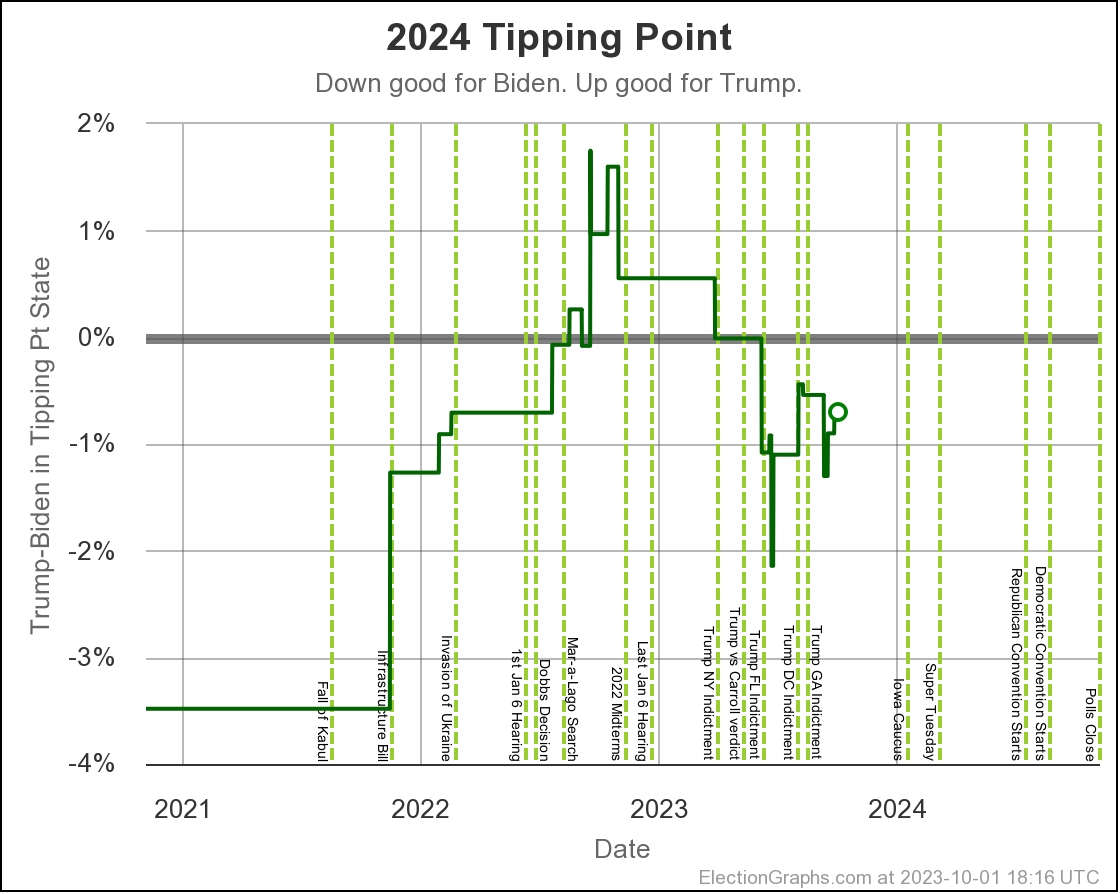
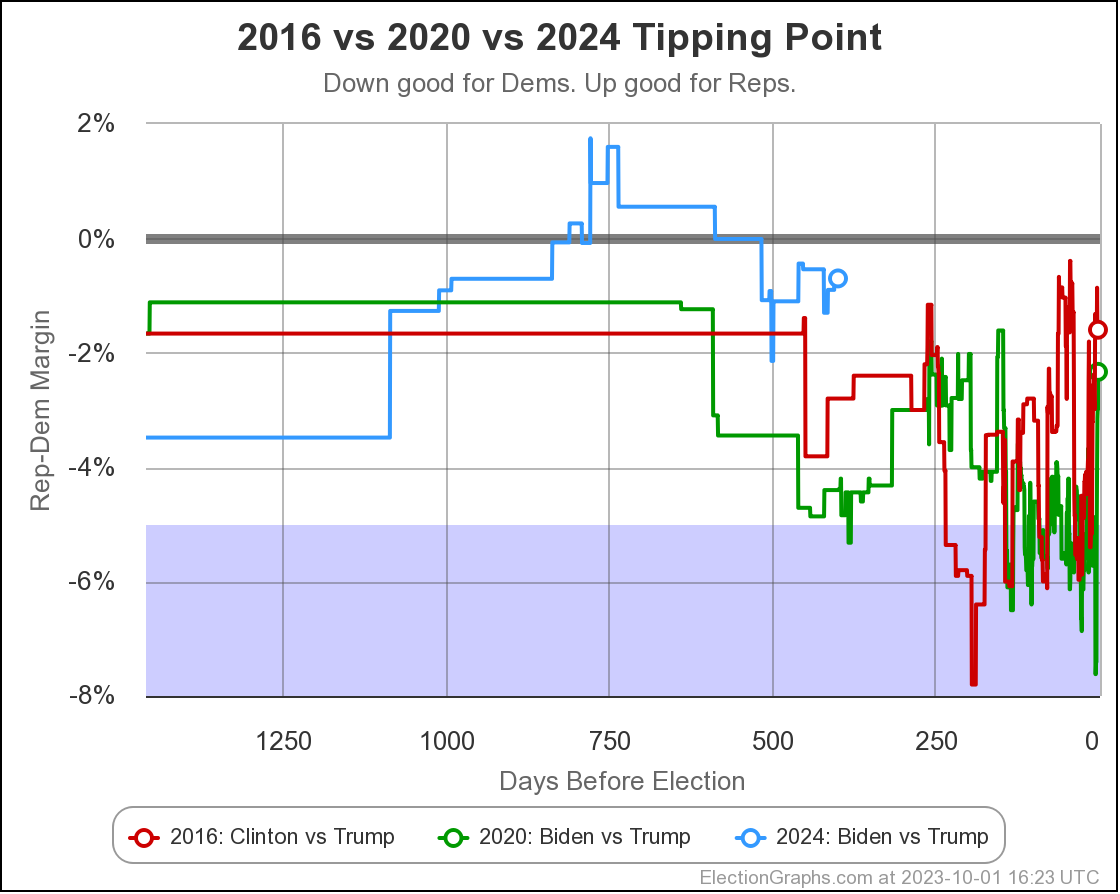
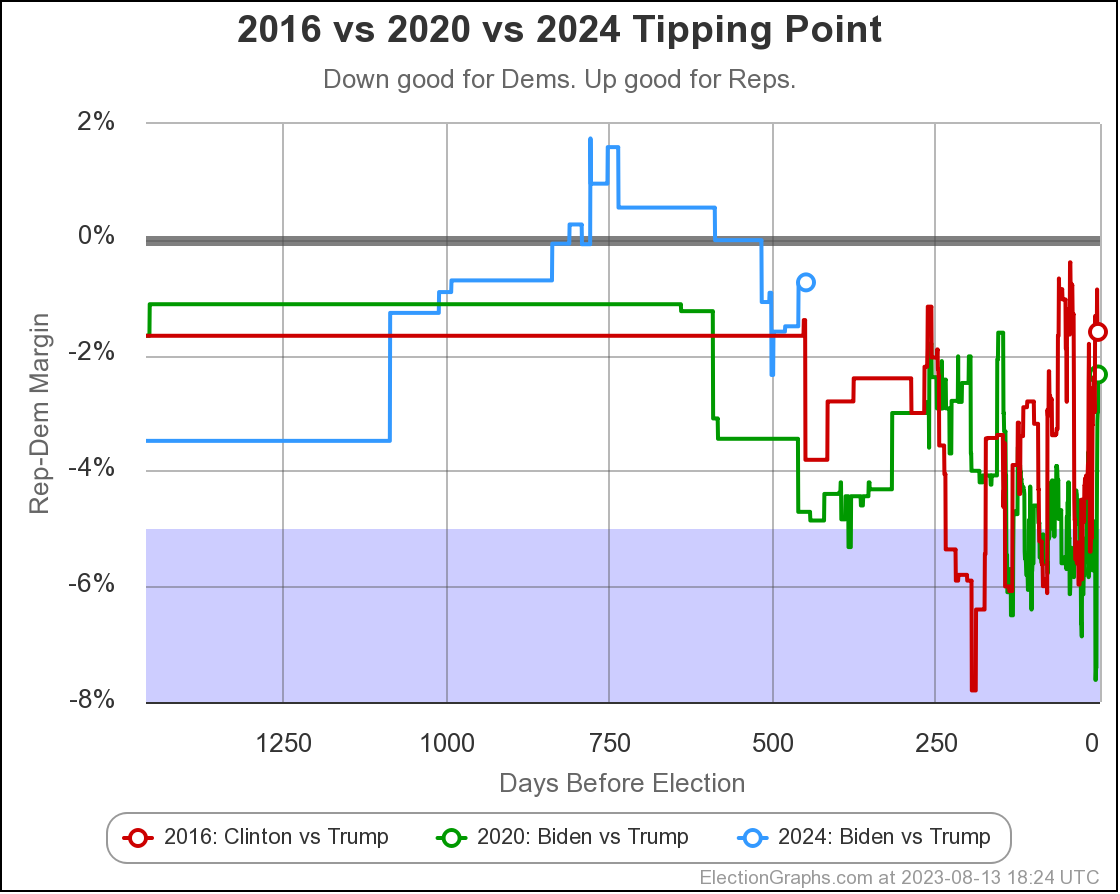
A better way to understand this "straight poll averages" view doesn't look at the electoral college margin, but instead how much the margin would have to change in the tipping point state to change the winner. Here is some history on the tipping point margin:

• 2023-03-25: Trump by 0.7% in Wisconsin
• 2023-04-24: Trump by 0.5% in North Carolina
• 2023-05-21: Trump by 0.2% in Wisconsin
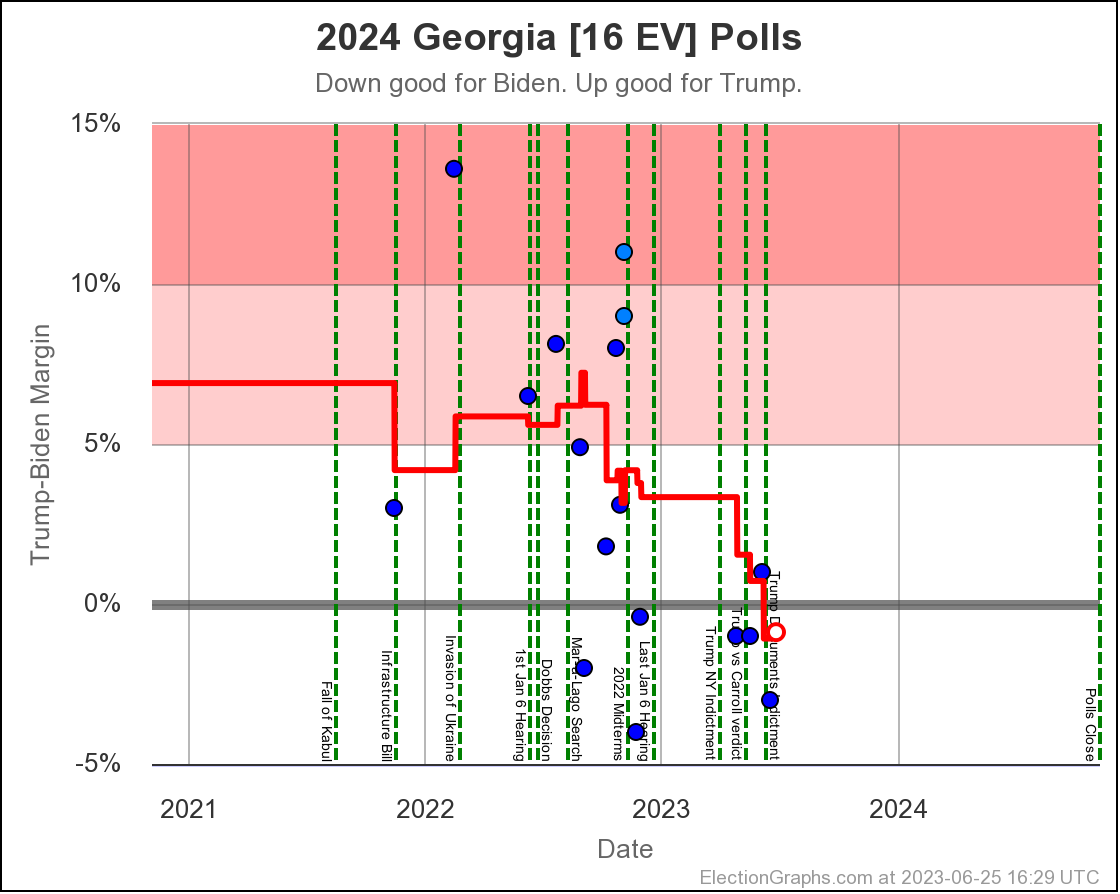
• 2023-06-25: Biden by 0.9% in Georgia
• 2023-08-13: Biden by 0.7% in Michigan
• 2023-10-02: Biden by 0.7% in Pennsylvania

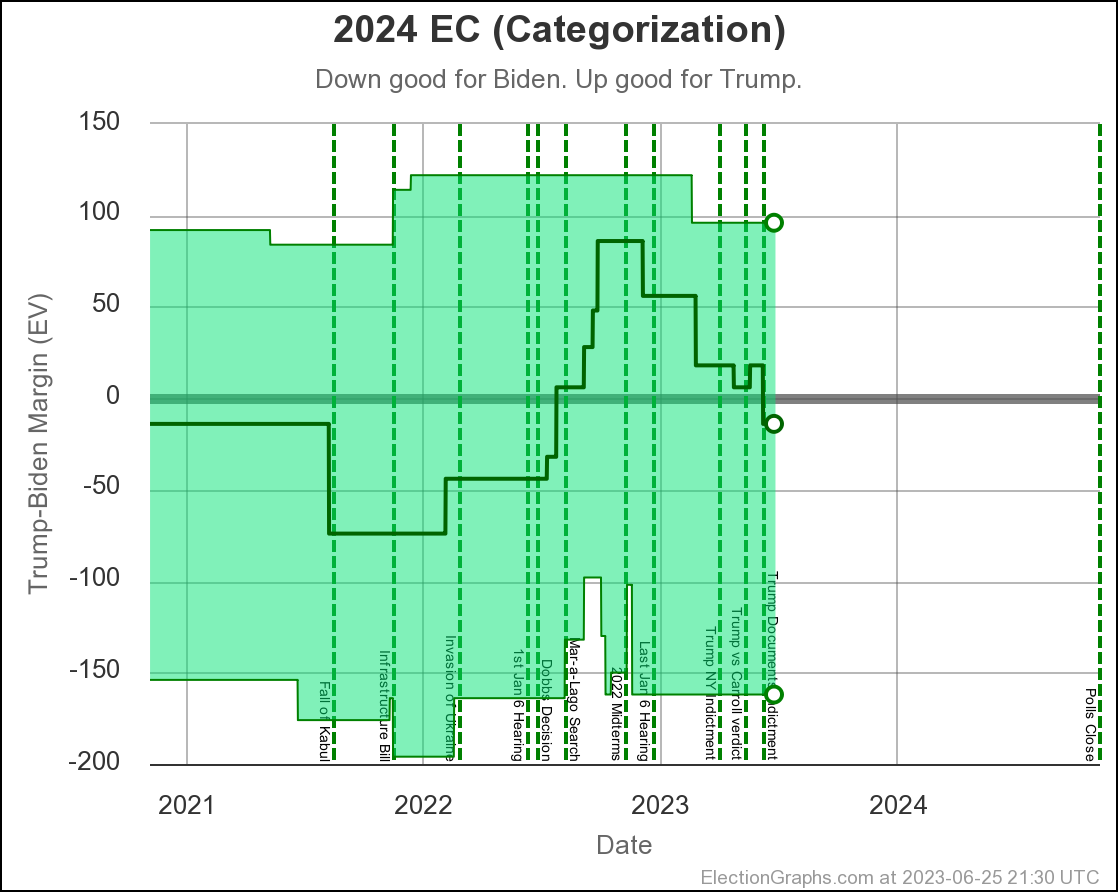
And here is a graph of how this has evolved:

The picture of course matches the others. At the moment Biden leads in the state that would put him over the edge (Pennsylvania at the moment) by only 0.7%.

Leads that small are ephemeral, and possibly illusory.

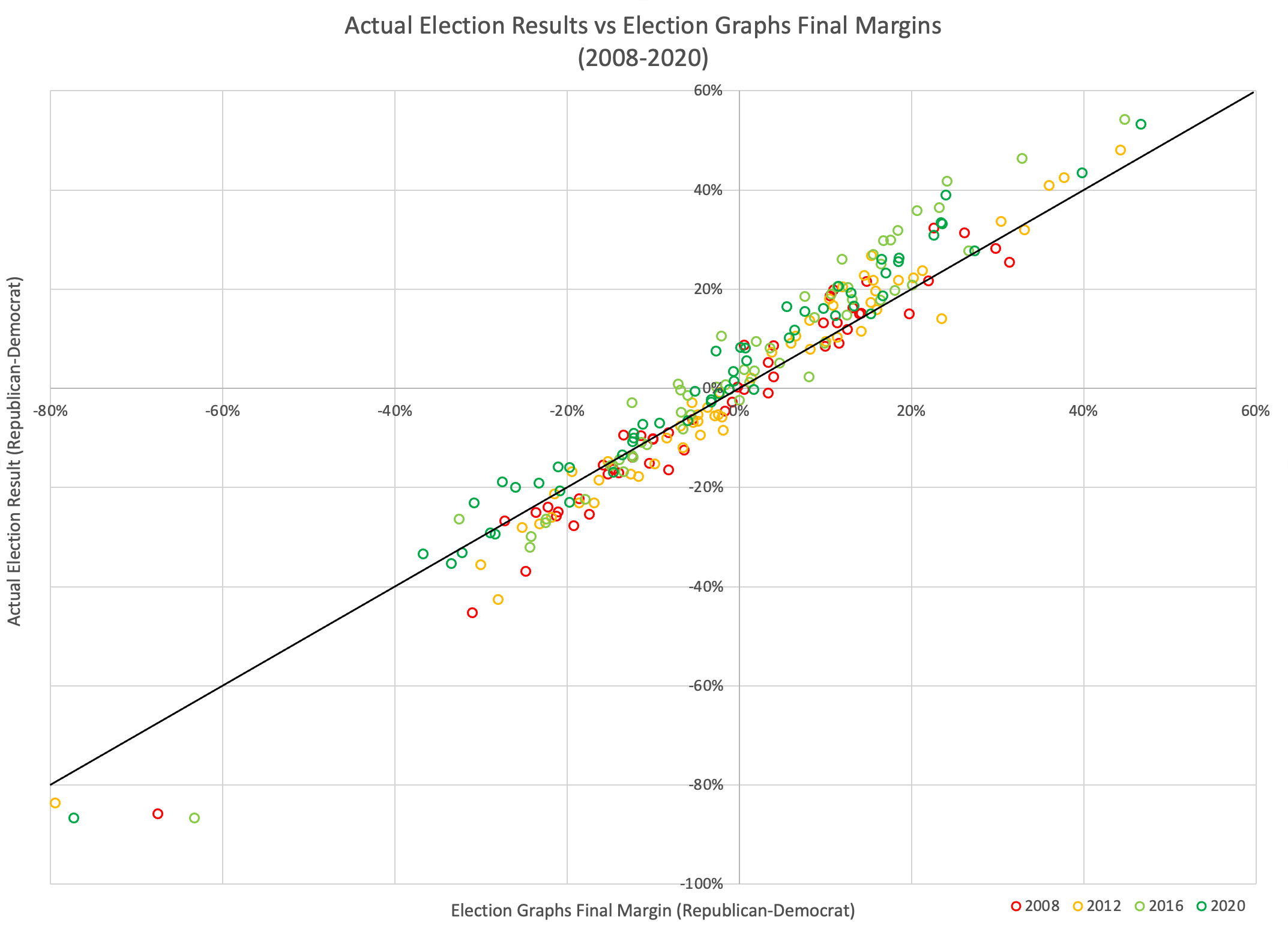
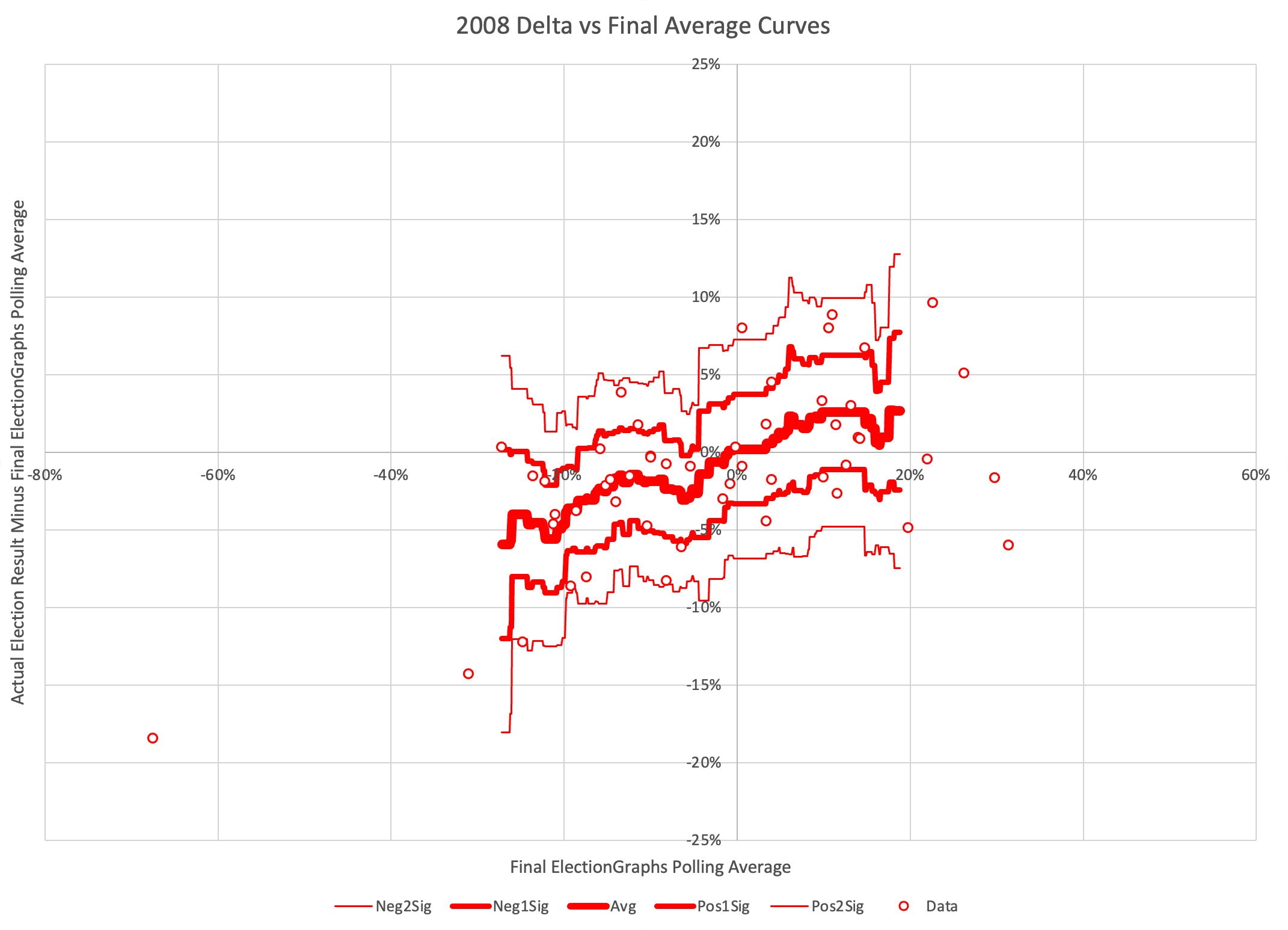
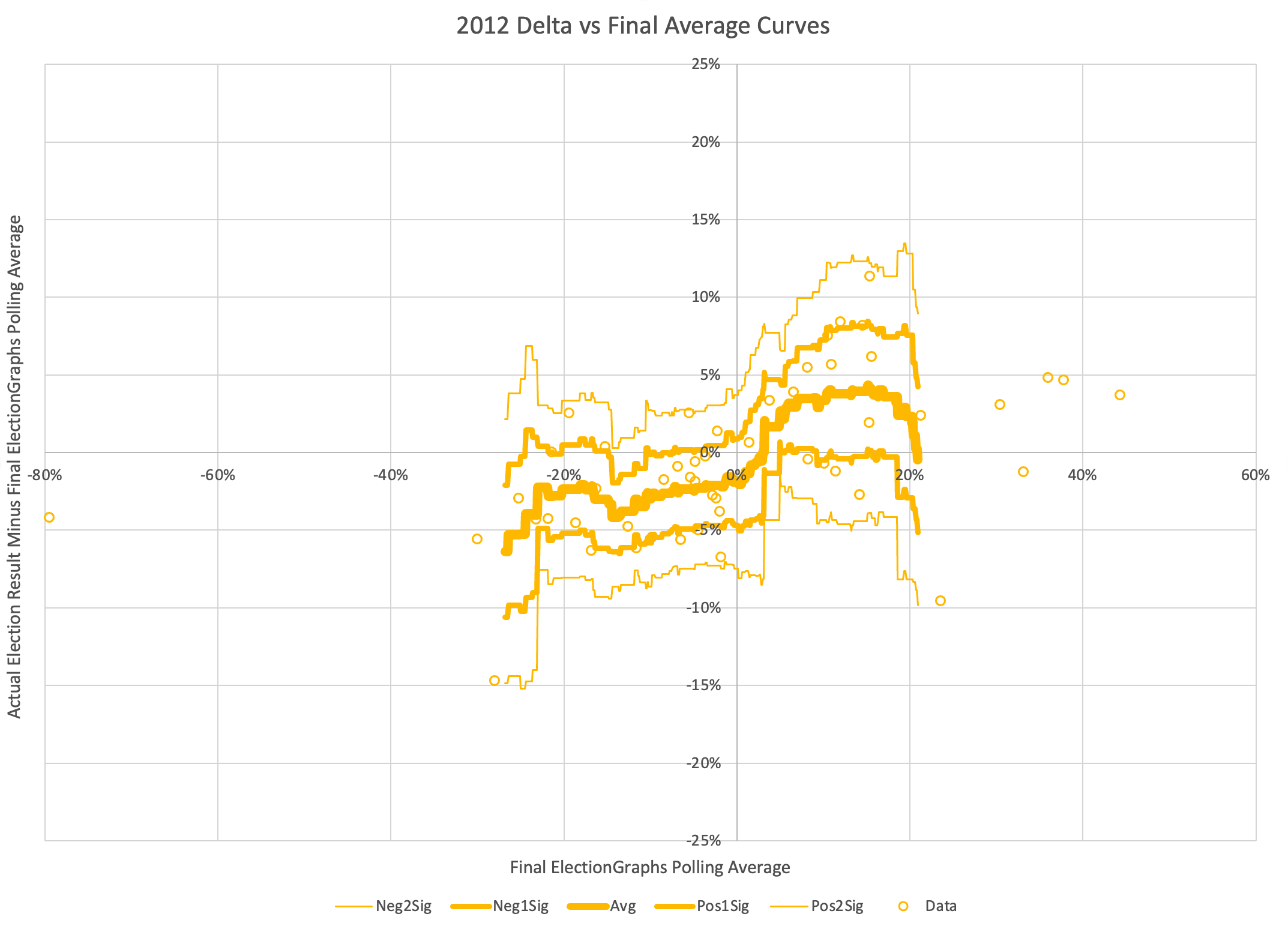
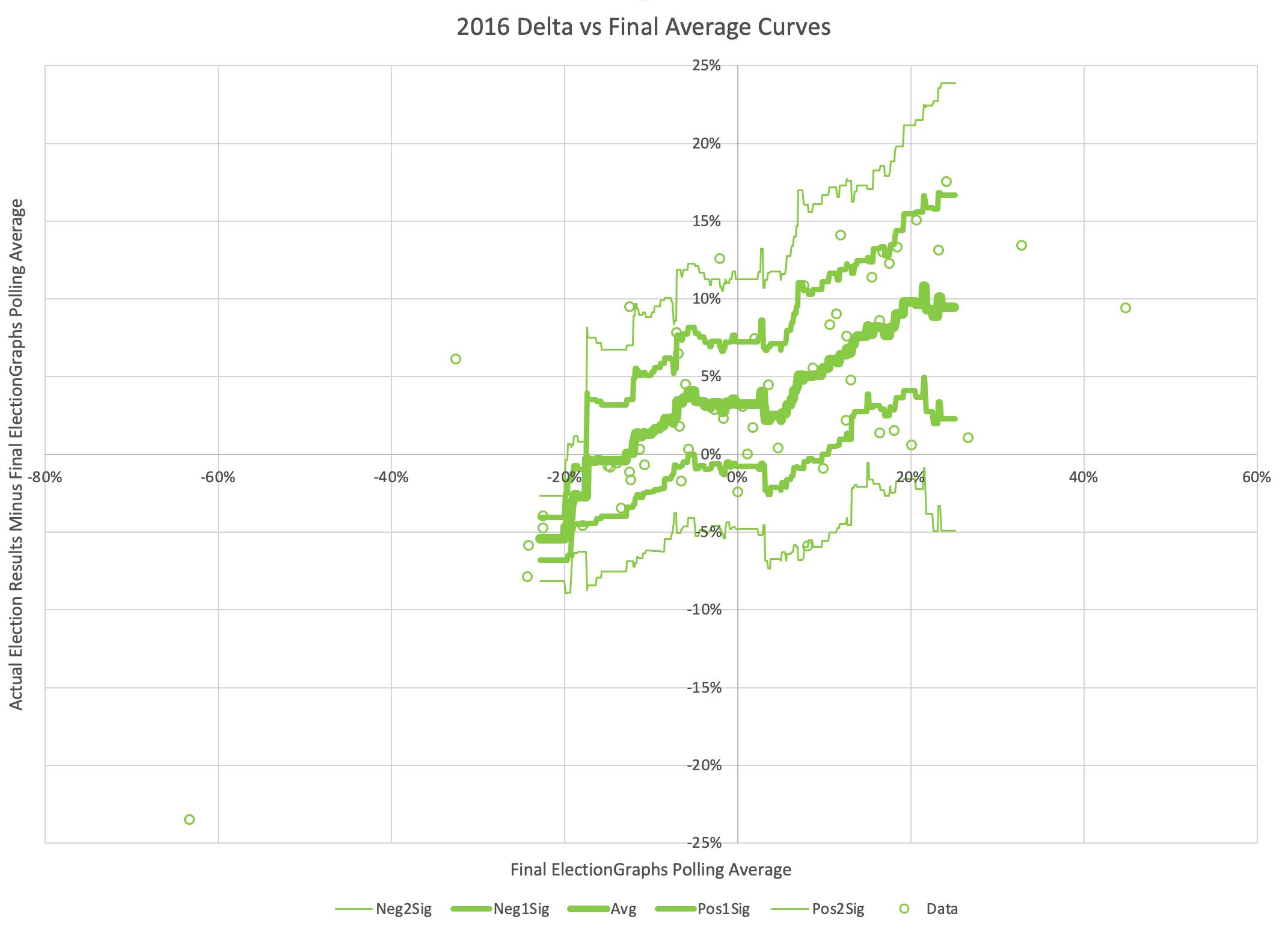
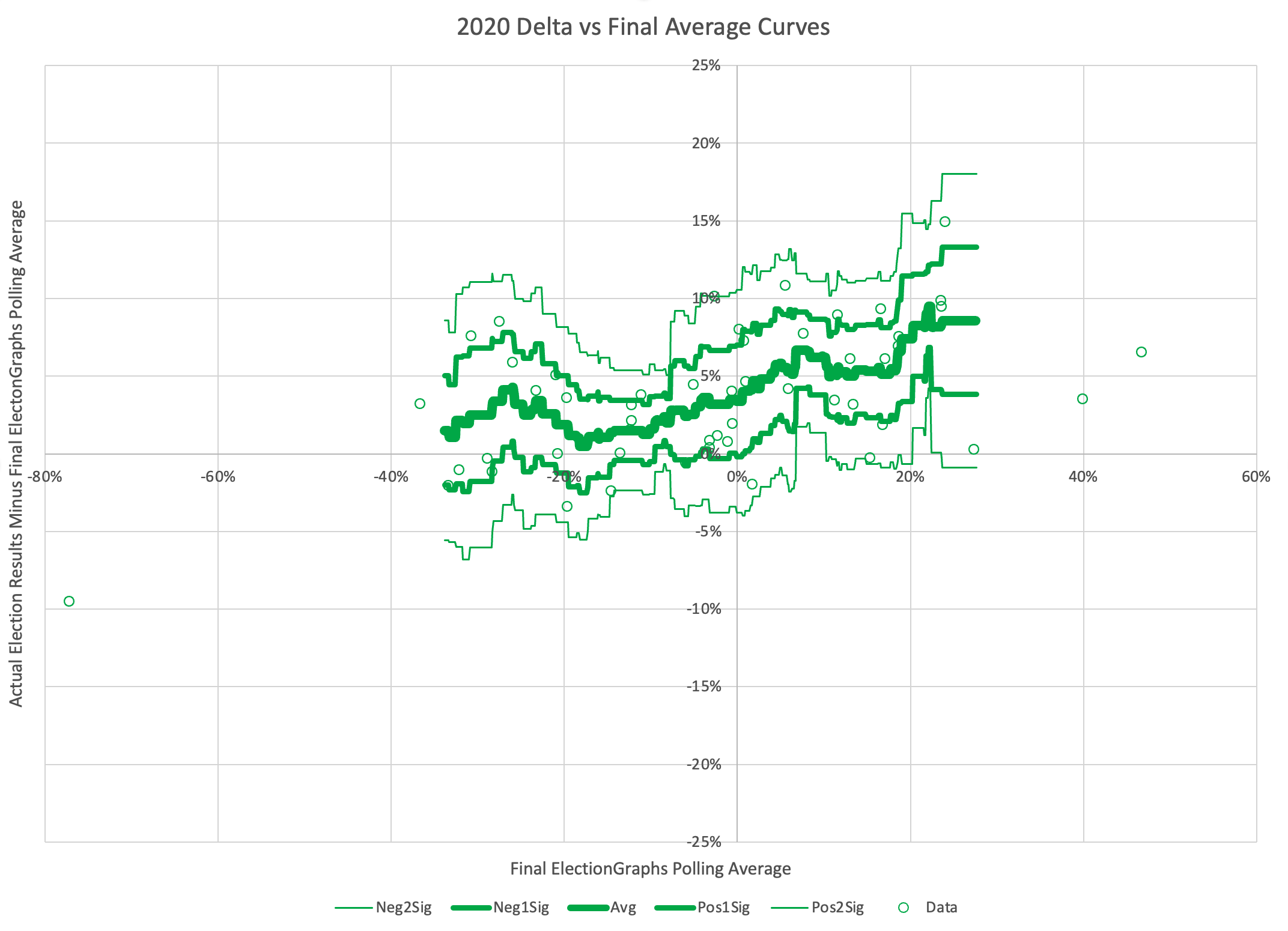
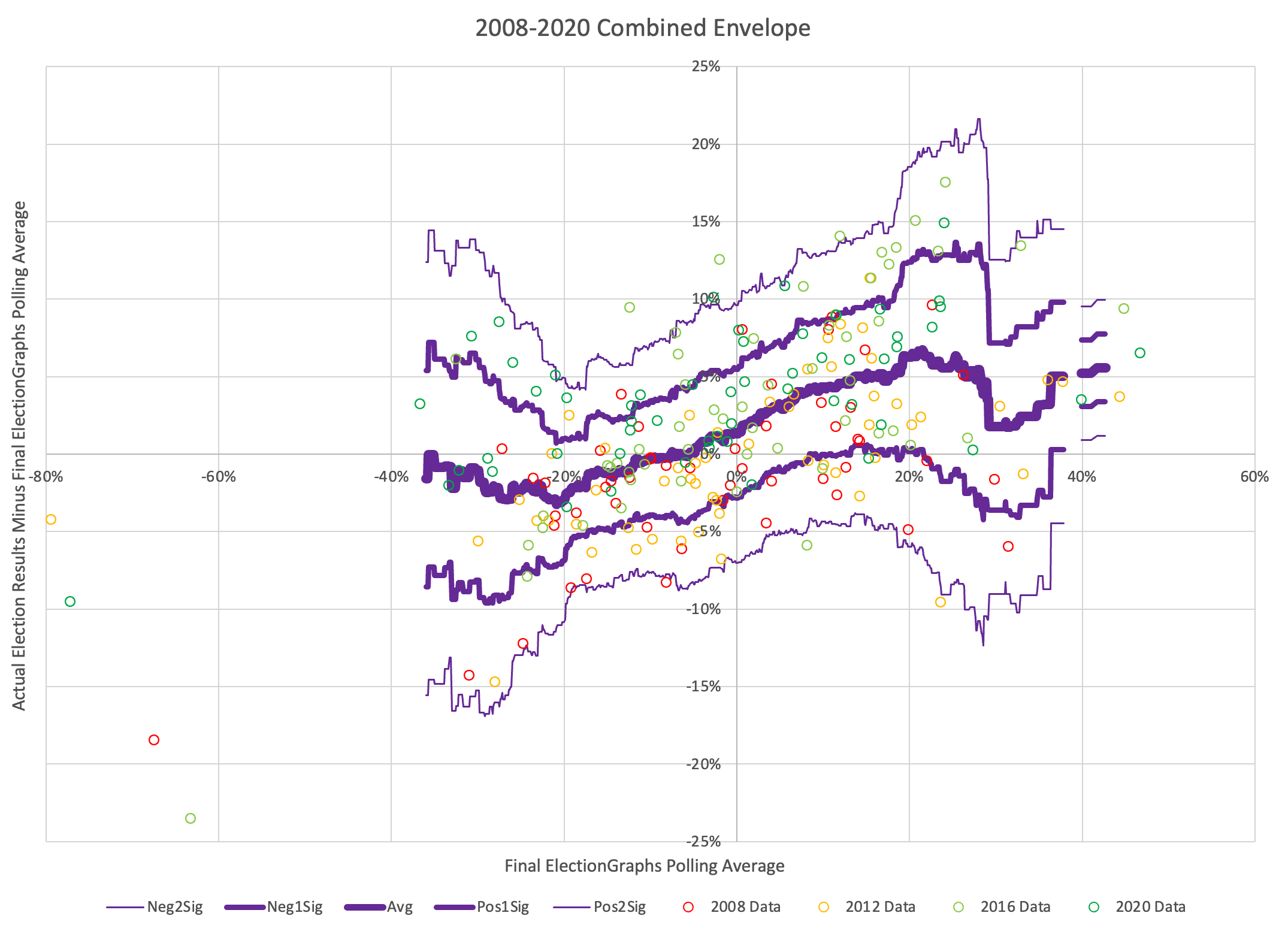
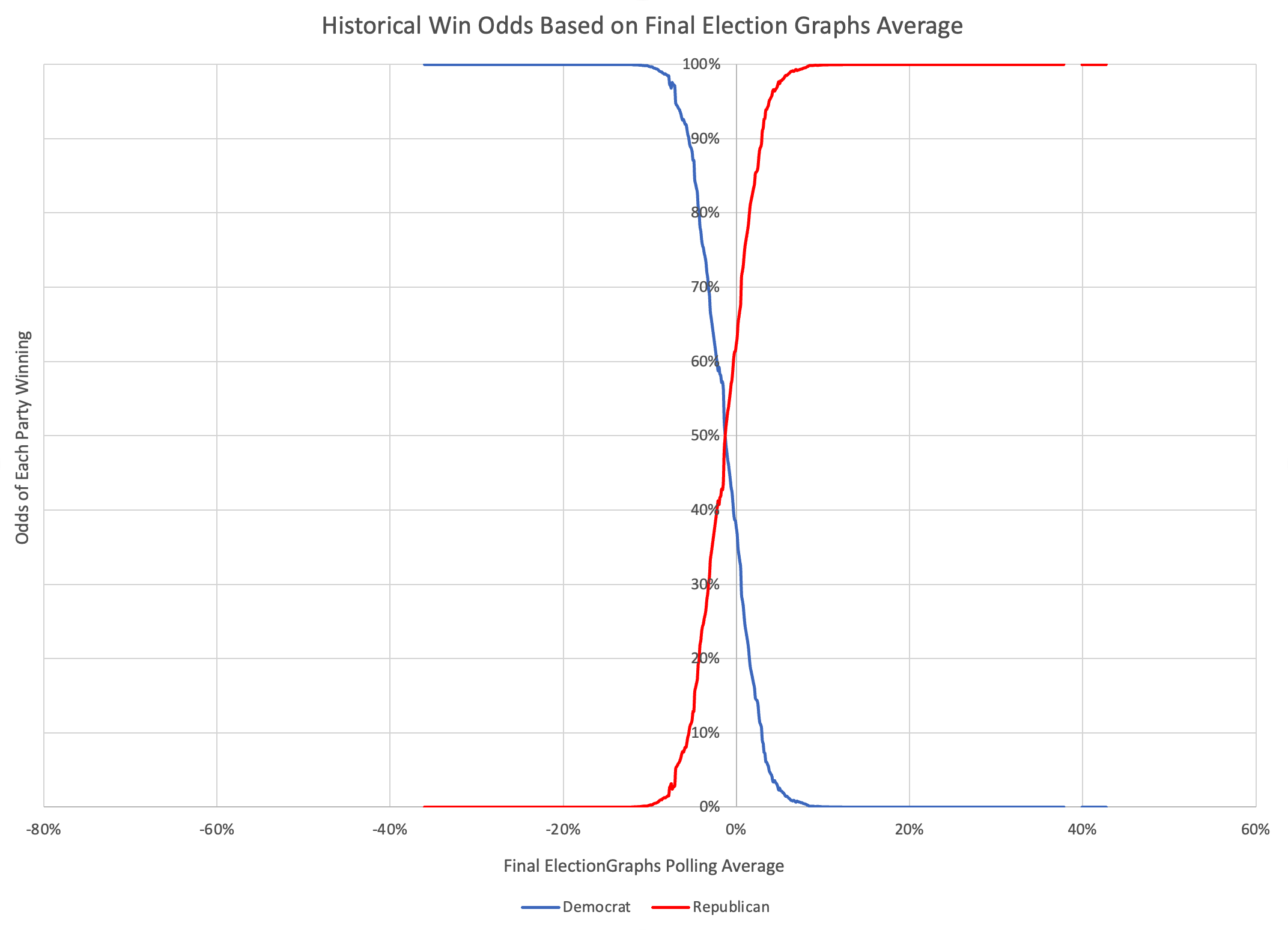
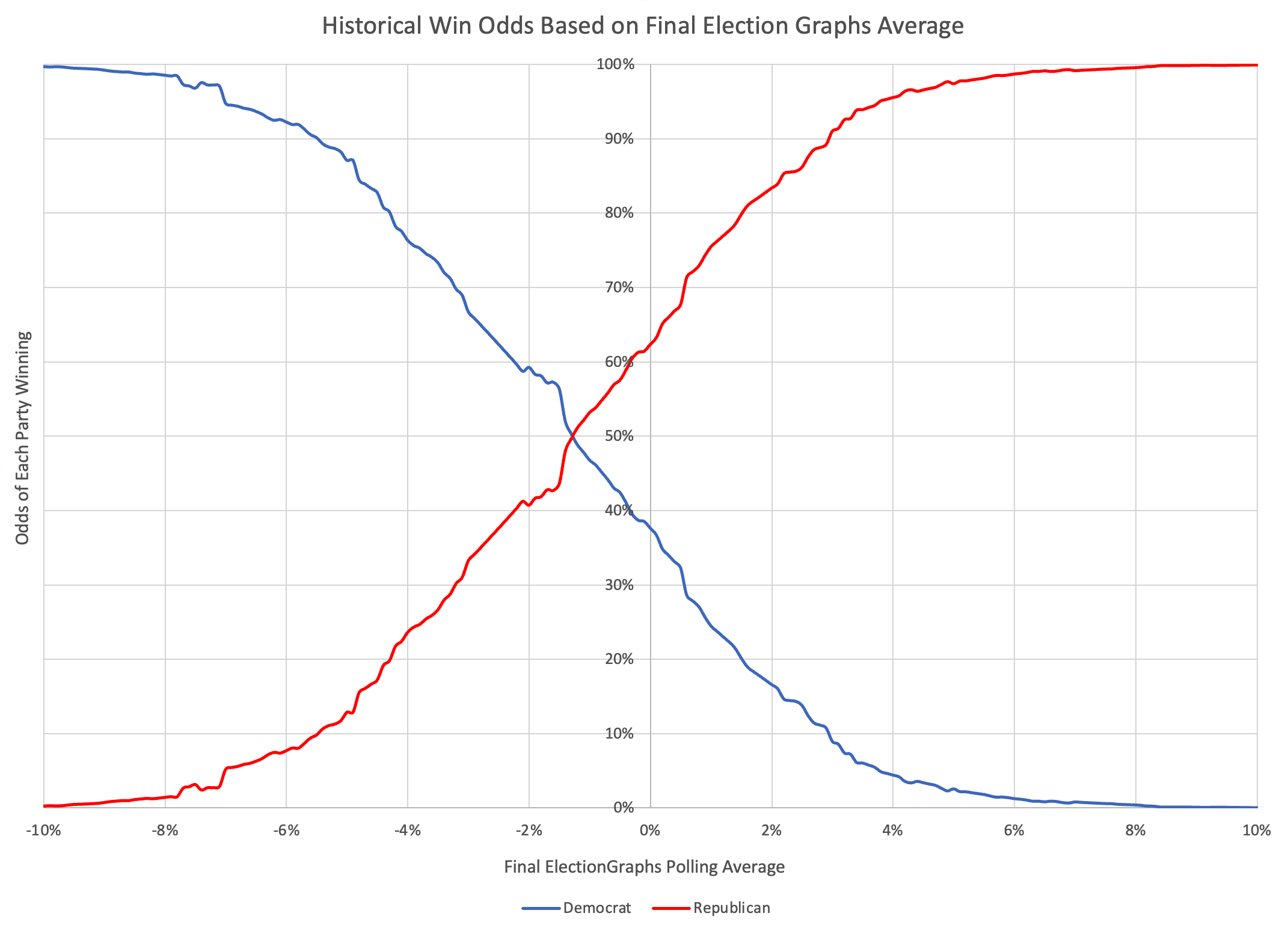
The probabilistic views here are all based on looking at the final election graphs averages in all the states compared to the actual election results in 2008 through 2020. Basically, in cases where Democrats were ahead by about 0.7%, they won only about 44% of the time.

So with Biden leading by 0.7% in the tipping point state, this is why the two probabilistic views give Trump an edge, even though the straight up poll averages give Biden a slight advantage.

Either way, the correct summary is "too close to call".

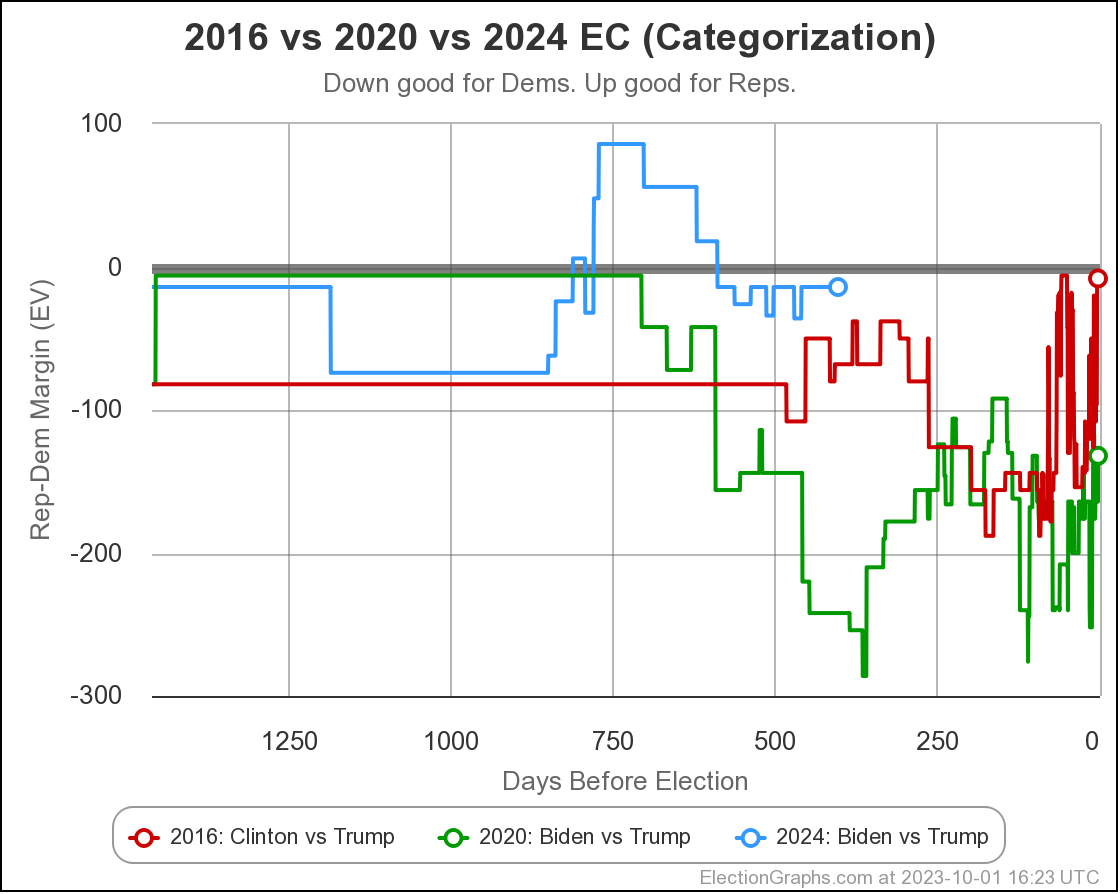
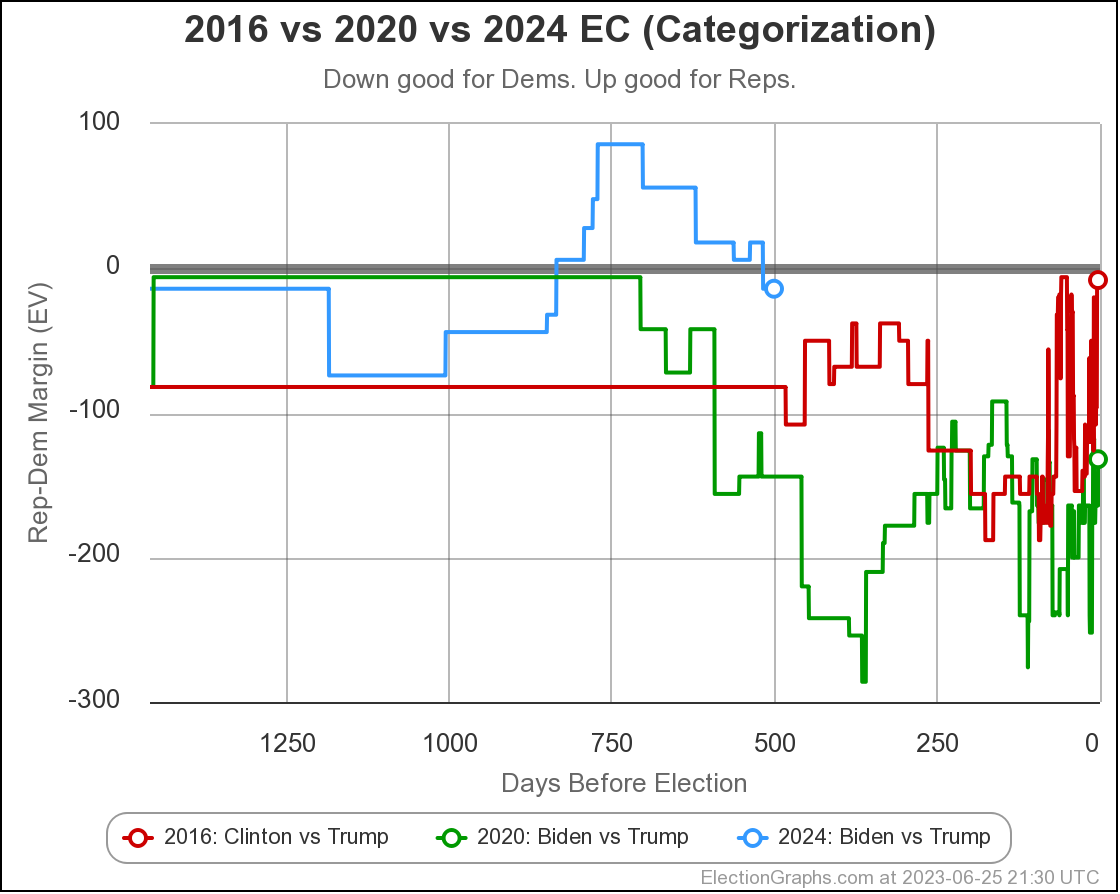
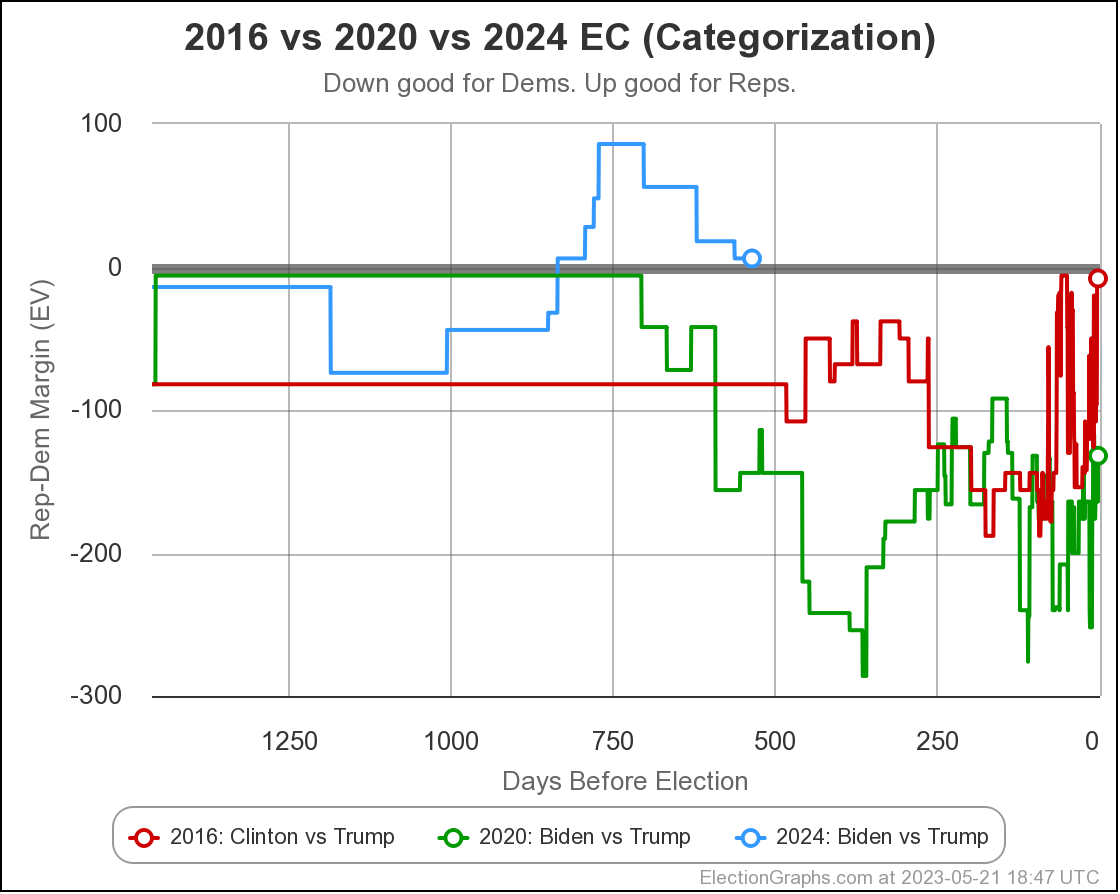
As usual, lets compare to 2016 and 2020 as well:

There are some arguments to be had related to Democratic over performance in midterms and special elections that while the polls may have underestimated the Republicans in 2016 and 2020, they may be underestimating the Democrats in 2024 like they did in 2012.

Maybe. There will be no way to tell until the votes are counted.

But at the moment, Biden continues to not only be weaker than he was against Trump in 2020, but in fact significantly weaker than Clinton was at the same point in 2016. There is a long time to go yet, but the Biden camp should not be happy with this position. Trump on the other hand should be heartened. Even with all of his mounting legal issues, he looks to be in a relatively strong position. For now anyway.

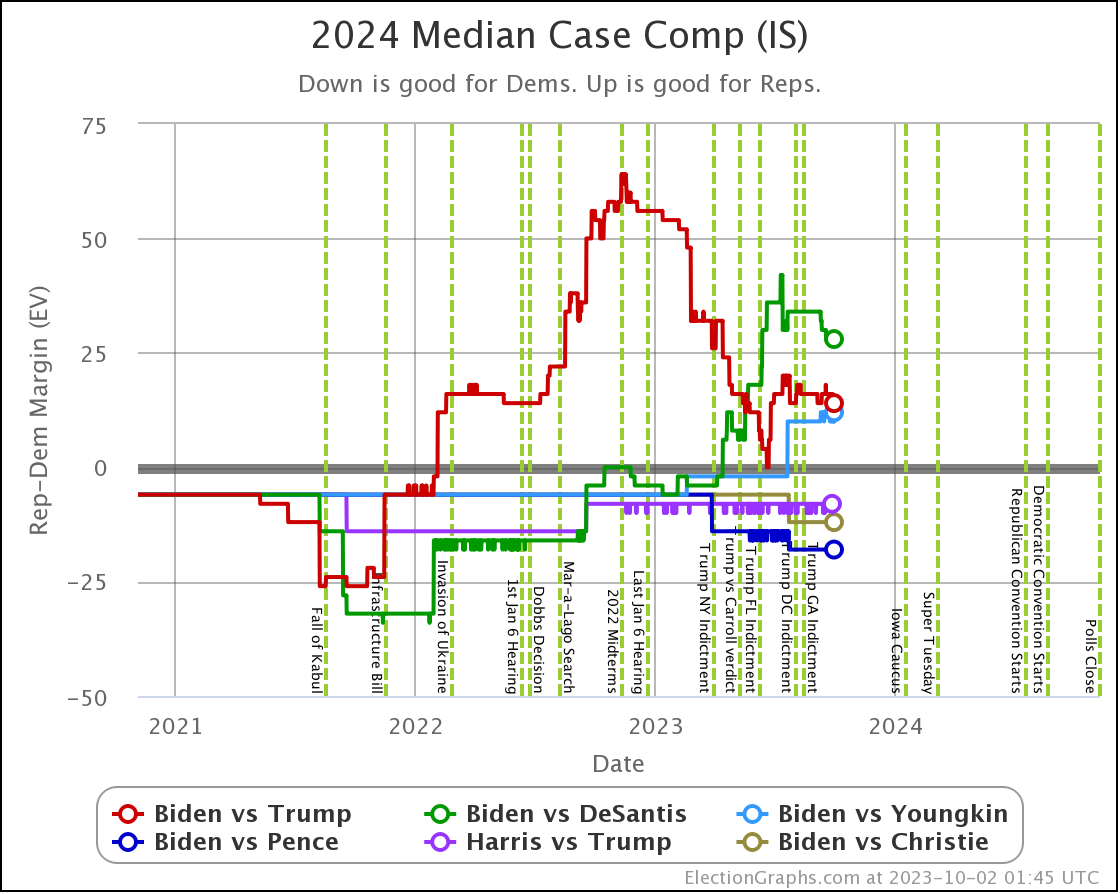
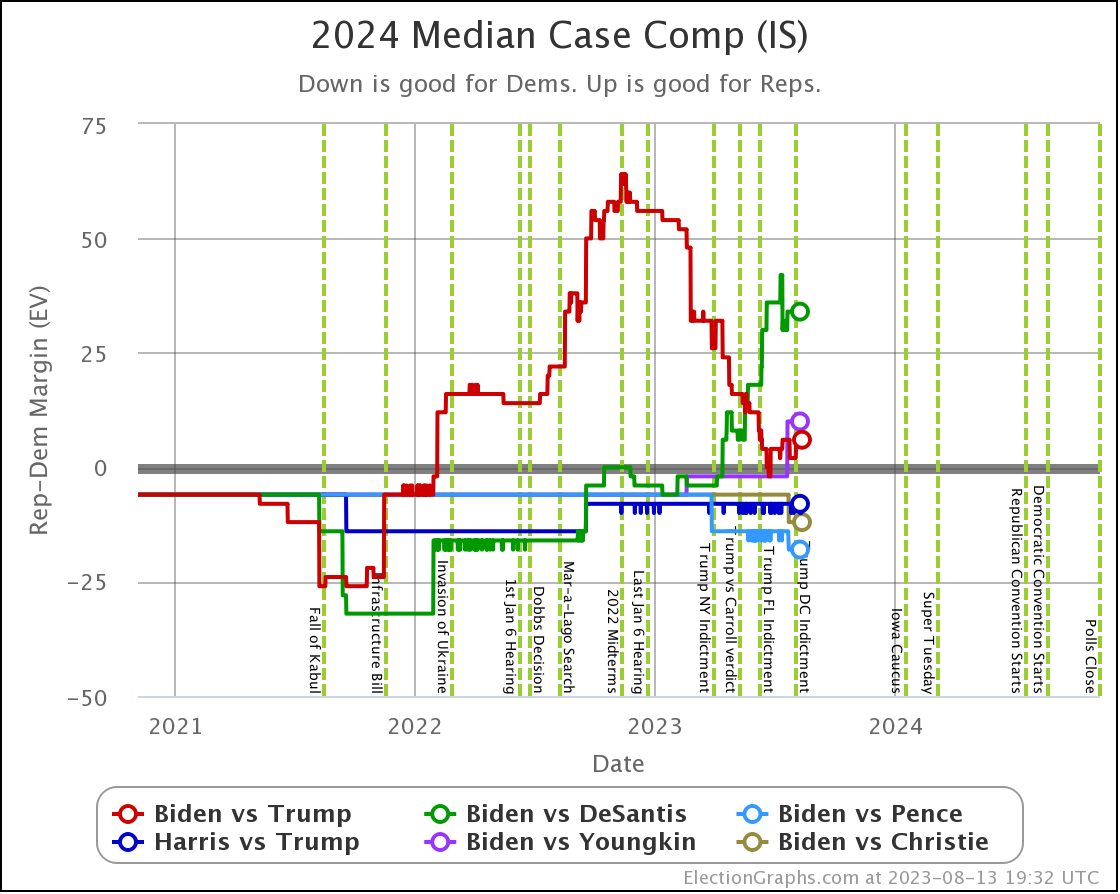
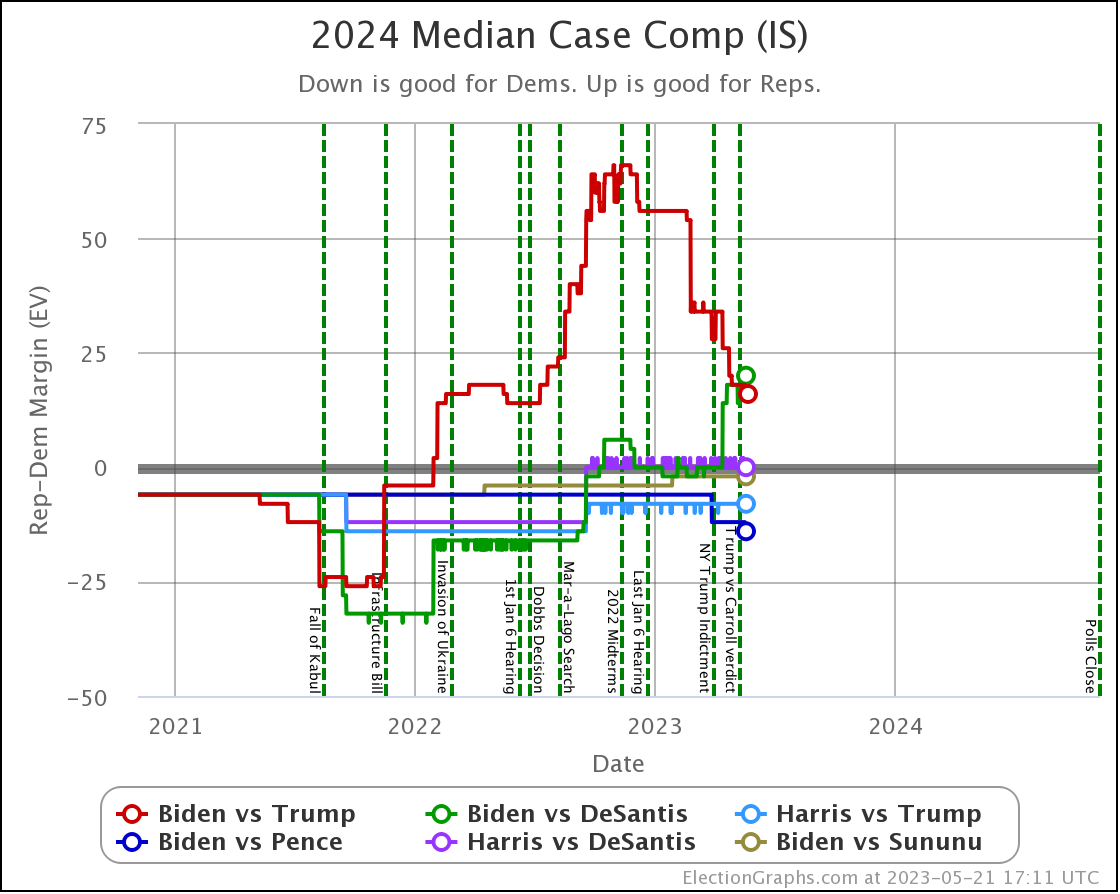
What if it isn't Biden vs Trump? OK, a quick look…

The above compares the median electoral college margin in the Independent States view between the 6 best polled candidate combinations.

Of these six though, Biden vs Trump is STILL the only one where I would say we have good reliable data.

Biden vs DeSantis is getting closer, but still needs to be taken with a grain of salt. There are still lots of "close states" where there haven't even been five polls yet.

And the other four combos on this chart? Just ignore them completely. There are only a smattering of polls on those combinations, not anywhere near enough to even remotely believe anything we see yet.

With those caveats, DeSantis does look stronger against Biden than Trump does on this chart at least.

Odds wise the Independent States view gives Biden only a 19.2% shot against DeSantis compared to 35.6% against Trump.

Looking at the Uniform Swing view however gives Biden a full 57.3% against DeSantis, better than his 44.2% against Trump.

So there is still a lot more uncertainty in the DeSantis picture.

Right now primary polling indicates both Biden and Trump are cruising to their respective nominations. If this ever changes, we'll pay more attention to the other possible combinations and dig a bit deeper.

For full Biden vs DeSantis info, look here.

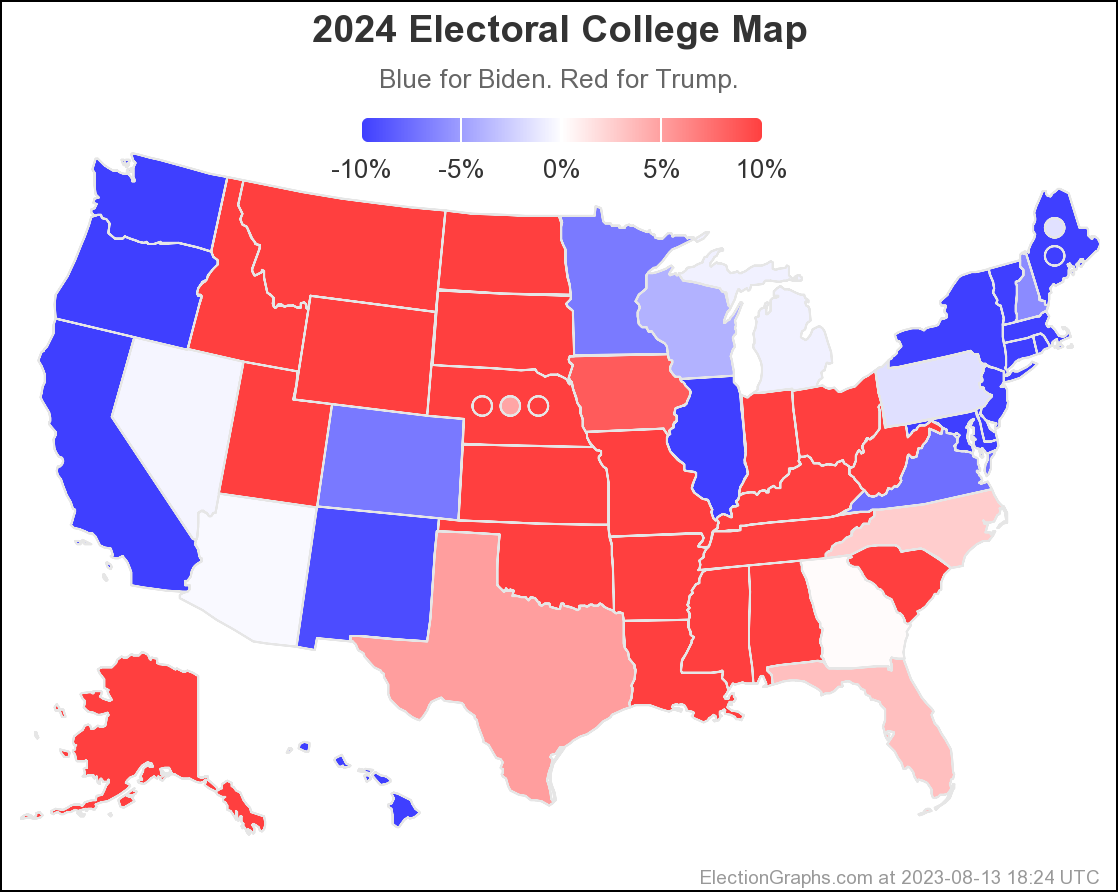
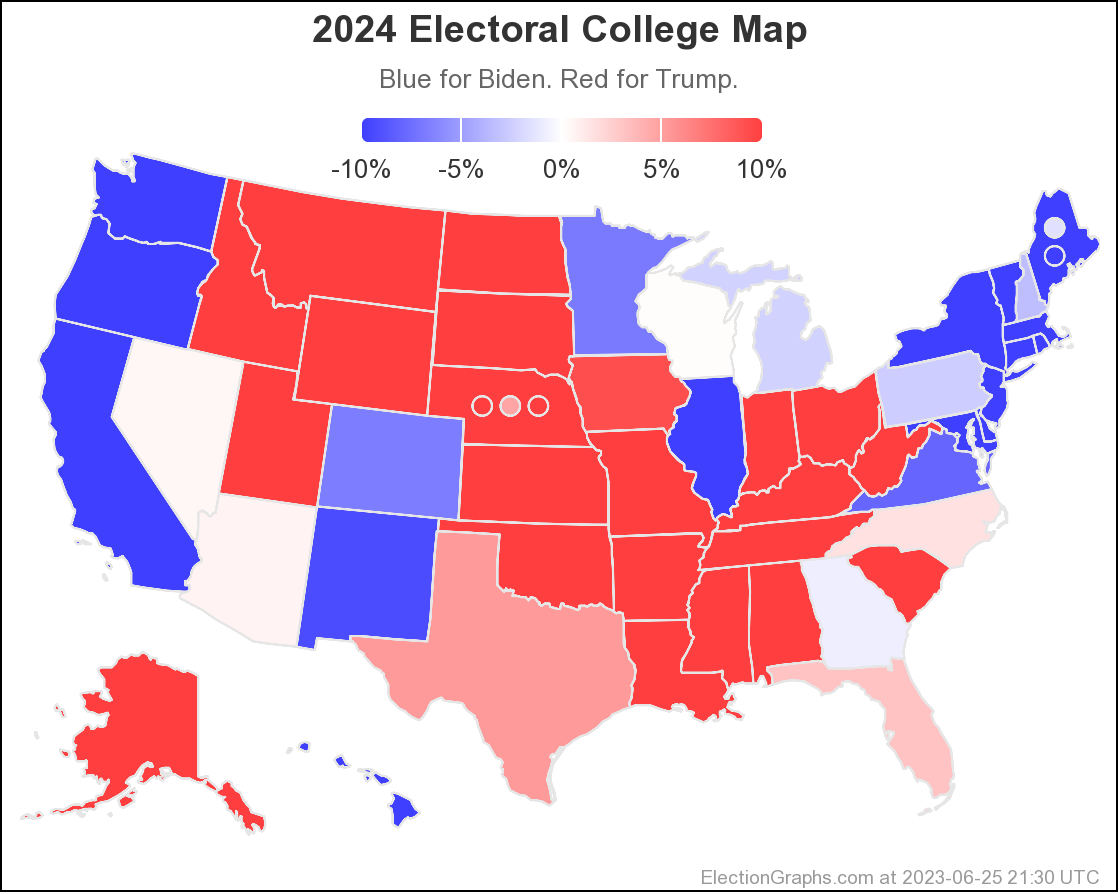
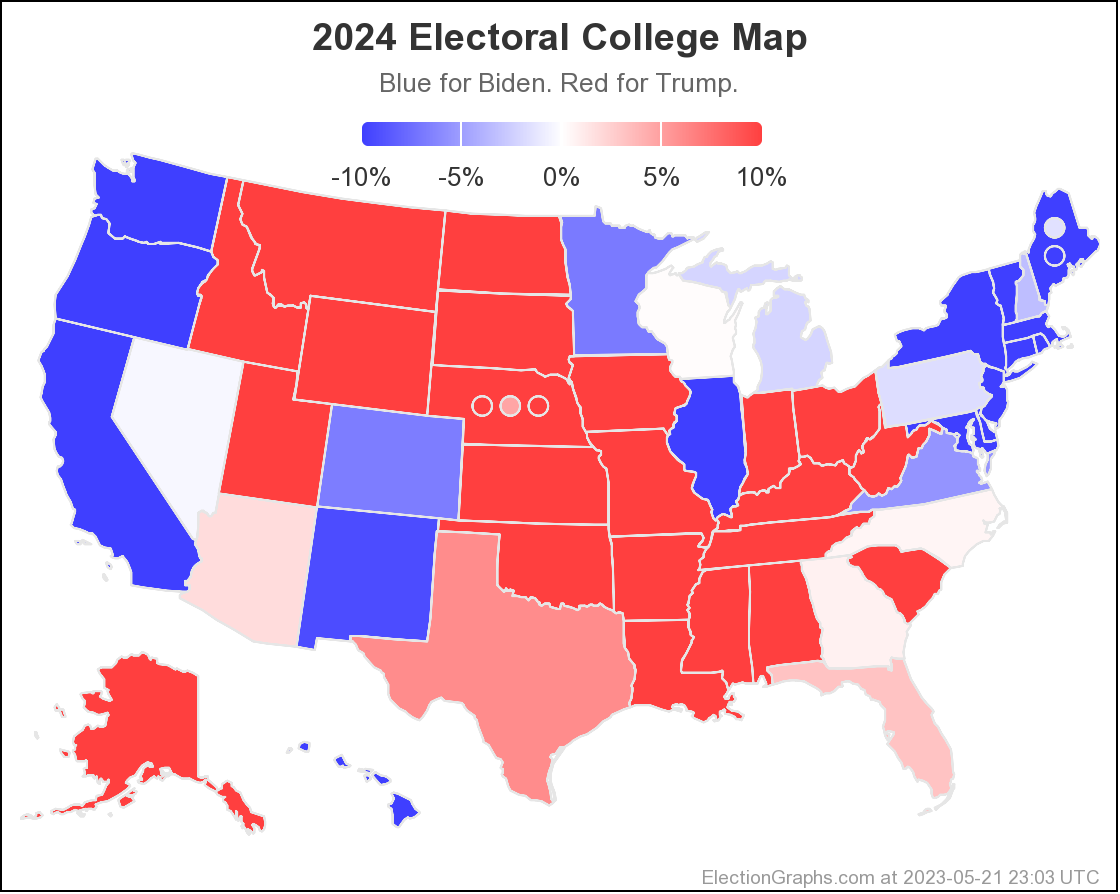
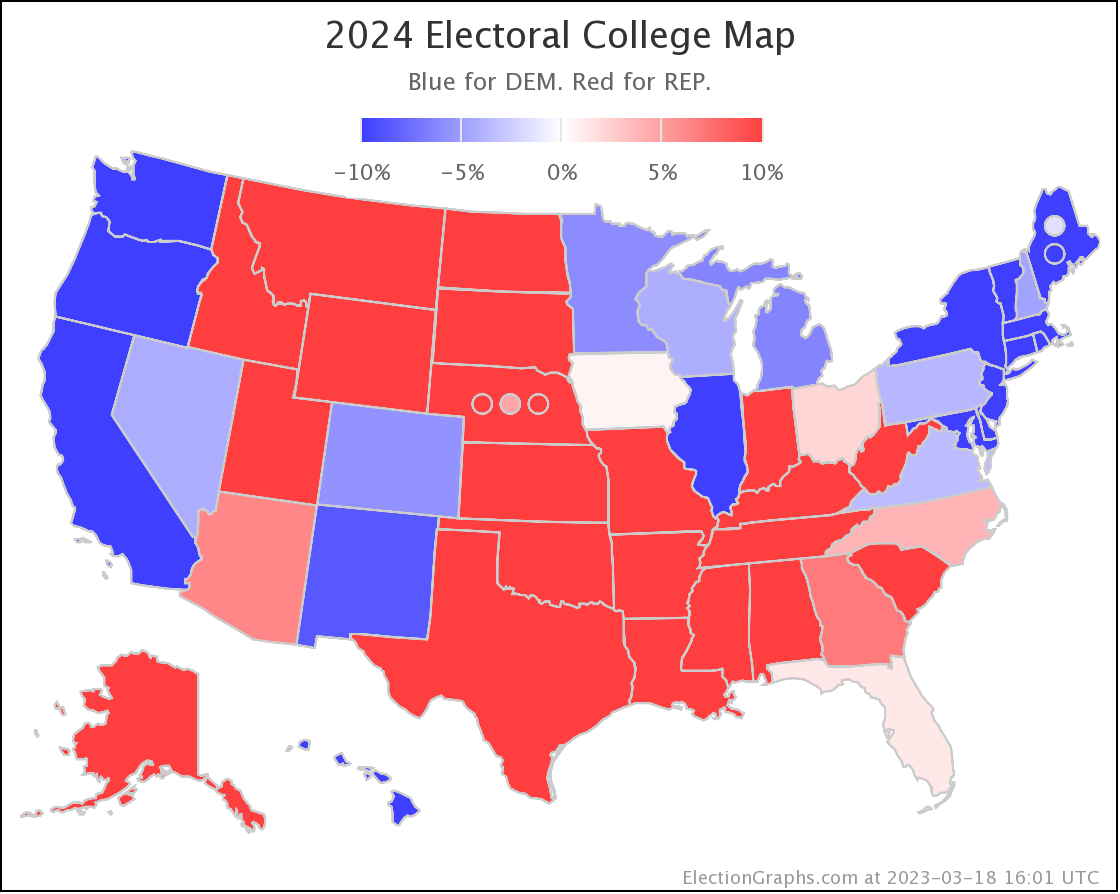
As I always do, I'm going to end with the current national Biden vs Trump map:

400.8 days until polls start to close on Election Night 2024. Hang tight.

I had hoped to do another update four weeks after the last one, but here it is about 50 days after my last post instead. Life gets in the way. Oh well. But it does mean that this update is right on the 450 days away from polls closing mark. So there is that.

The quick summary for those who don't want to read all the details:

• Once again, if a Biden vs Trump election was held today (it won't be), it would be fundamentally too close to call.
• Biden's odds are slightly less than they were last time, but in between that update and this one, he was better off, so things have at least leveled off, and may have started moving in Trump's direction again.
• Biden has a lead if you take the state poll averages at face value, but this relies on several states where his lead is less than the average amount polls have underestimated Republicans in close states from 2008 to 2020, so be wary of trusting those leads.
• Because of the above, both of my probabilistic views give a slight advantage to Trump despite the face value result.
• Biden's polling is weaker than both his own polling in 2020, and Clinton's polling in 2016 at the same amount of time before the election.

If you want updates on each and every poll as it comes out, as well as daily summaries of the status for the best polled matchup (currently Biden vs Trump), follow Election Graphs on Mastodon.

OK, now all the details that only the die hard will be interested:

New polling added since 2023-06-25:

• 24 Biden vs Trump: MIx4, AZx3, NVx2, PAx2, WIx2, NHx2, OHx2, NY, TN, FL, GA, NC, CA, VA, KY
• 11 Biden vs DeSantis: MIx2, OHx2, NH, WI, TN, NV, FL, AZ, VA
• 2 Biden vs Scott: NH, OH
• 1 Biden vs Pence: OH
• 1 Biden vs Haley: OH
• 1 Biden vs Christie: OH
• 1 Biden vs Youngkin: VA
• 1 Kennedy vs Trump: NH
• 1 Kennedy vs Scott: NH

Also, after going back and forth a bit on how much I wanted to do it this cycle, I decided that like previous cycles, when a pollster releases multiple versions of their results, like one for Registered Voters and one for Likely Voters, or they do "Definite" supporters vs "Total" supporters or what not. When this happens, I include both versions of the poll, but I weight them so the "sub-polls" together have the same weight as a single poll.

So I've been slowly going back and reviewing older polls I have in my system, and checking to see if they have these sorts of multiple results, and if so I've been adding the "half-polls" I missed originally. I'm slowly catching up with the current day as I do this. All of the below were old polls that I have updated.

• 31 Biden vs Trump: IAx4, AZx3, GAx3, PAx3, FLx2, MIx2, WI, CO, WA, AR, KS, LA, MS, MT, OH, OK, RI, SC, TX, NC
• 20 Biden vs DeSantis: AZx2, GAx2, PAx2, AR, FL, KS, LA, MS, MT, OH, OK,  RI, SC, TX, NC, IA, MI
• 1 Biden vs Pence: NC

As has been the norm the last few updates, I start with looking at the changes to the "spectrum of close states":

As it was on 2023-06-25:

And now on 2023-08-13:

The states where the poll average moved toward Trump are:

• Michigan (15 EV): Biden by 2.3% -> Biden by 0.7% (Trump+1.6%)
• North Carolina (16 EV): Trump by 1.5% -> Trump by 2.6% (Trump+1.1%)
• Georgia (16 EV): Biden by 0.9% -> Trump by 0.2% (Trump+1.1%)
• Pennsylvania (19 EV): Biden by 2.6% -> Biden by 1.6% (Trump+1.0%)
• Virginia (13 EV): Biden by 8.0% -> Biden by 7.5% (Trump+0.5%)
• Florida (30 EV): Trump by 3.1% -> Trump by 3.3% (Trump+0.2%)

And the states where the poll average moved toward Biden are:

• Colorado (10 EV): Biden by 6.8% -> Biden by 7.0% (Biden+0.2%)
• Texas (40 EV): Trump by 5.2% -> Trump by 5.0% (Biden+0.2%)
• Iowa (6 EV): Trump by 9.2% -> Trump by 8.5% (Biden+0.7%)
• Arizona (11 EV): Trump by 0.6% -> Biden by 0.3% (Biden+0.9%)
• Nevada (6 EV): Trump by 0.5% -> Biden by 0.5% (Biden+1.0%)
• New Hampshire (4 EV): Biden by 3.4% -> Biden by 6.0% (Biden+2.6%)
• Wisconsin (10 EV): Trump by 0.2% -> Biden by 4.0% (Biden+4.2%)

The last few (roughly) monthly updates have been very lopsided, with a lot more states moving toward Biden than moving toward Trump from this group of close states. (We really don't care about how states move if one candidate has an overwhelming lead.) This time though, 7 states moved toward Biden, 6 states moved toward Trump. That is much more even, indicating we've moved into a more stable period, at least for a little while.

Georgia, Arizona, and Nevada crossed the center line.

Let's look at them in more detail.

This time I won't write a paragraph of commentary on each state, you can look above and draw your own conclusions.

At the moment these are the three closest states according to the straight up averages though, all with margins 0.5% or less. You can expect the closest states to bounce around from one side of the center line a bit.

OK, lets look at the overall summary:

Looking at the evolution of the Biden win odds first:

• 2023-03-25: Between 17.8% and 25.8%
• 2023-04-24: Between 24.9% and 32.3%
• 2023-05-21: Between 34.9% and 35.9%
• 2023-06-25: Between 43.9% and 46.0%
• 2023-08-13: Between 42.9% and 44.2%

The trend of Biden being stronger each time than the time before has been broken, with Biden slightly weaker this time than last. Lets look at the two odds charts to see if we can get any additional insights.

In both ways of calculating odds (the two extremes of how correlated state polling errors might be) you can see that for a time the odds actually favored Biden for a bit, but then things popped back in Trump's direction. The net result is that we are pretty close to where we were in the update 50 days ago, but the trend has reversed.

Now is this move toward Trump something that will be sustained? Or is it just a temporary blip before the trend toward Biden continues? Of course there is no way to know other than to wait and see what happens next.

So how does this look in terms of the electoral college? Here are the three views:

The first two are the two probabilistic views based on how correlated the state polling errors may be and taking into account how far off polls have been from the final election results in the past 4 election cycles. The third is just taking the state poll averages at face value.

But for all three the key is to not fixate on the green line in the center, but instead look at the green bands. For the probabilistic views there are graduations that don't exist in the categorization view, but in all three, there is a fair amount of green on both sides of the center line.

This means that either candidate winning is a reasonable outcome to consider, thus the summary that this race would be "too close to call" if the election was today.

It remains close. And in the last 50 days, movements have been mixed, so there isn't a clear trend either. Nobody is pulling away here.

Another way to look at the straight unmodified polls is to look at the "tipping point", which is how much you would have to shift all the polls to change the winner. It has been evolving like this:

• 2023-03-25: Trump by 0.7% in Wisconsin
• 2023-04-24: Trump by 0.5% in North Carolina
• 2023-05-21: Trump by 0.2% in Wisconsin
• 2023-06-25: Biden by 0.9% in Georgia
• 2023-08-13: Biden by 0.7% in Michigan

Just another way of showing a super close race.

Time to compare to 2020 and 2016:

Biden still lags where Clinton was at this stage in the 2016 cycle, and is far behind where he was himself in the 2020 cycle. Given the Trump win in 2016, for Biden to be feeling good, I'd think he would AT LEAST want to be doing better in the polling than Clinton was in 2016. He is not there right now.

I have heard many folks state things like "Biden vs Trump is a rematch, Biden won last time, so he will win again" or that "surely with all his legal issues, there is no way Trump can win".

It is unwise to make these sorts of assumptions.

Well, what if Trump's legal issues (or something else) at some point cause the Republicans to give the nomination to someone else? (Yes, I know he is way ahead on that front, but what if?)

The polling for Biden vs Trump is still the only combination where there have been enough polls in the close states that I feel confident making judgements on it. Most combinations just have scattered polling, so looking at the state by state info like we do here is almost meaningless at this point.

But Biden vs DeSantis is getting closer and closer to having good polling in the close states, so lets take a look anyway.

Here is a comparison of the medians for the Independent States probabilistic view:

He may be woefully behind in the Republican Primary polling, but for the general? He does better against Biden than Trump. At least in this view. (Again, still with much more limited polling, so the picture may be incomplete.)

Looking at probabilities from both probabilistic views, the picture is a bit more muddy. While we say Biden has between a 42.9% and 44.2% chance of winning, the spread is much bigger against DeSantis. The odds are anywhere from 15.9% to 57.3%. So basically, we don't really have a good handle on this particular match up.

The reason for such a wide spread between the probabilistic views is because of the specific configuration of close states and their averages for Biden vs DeSantis. If we get to the point where I feel the Biden vs DeSantis polling is more solid, AND it looks like the chances of that matchup are increasing, AND this situation persists by then, I will of course dive into that in more detail. But not today.

For full Biden vs DeSantis info, look here.

To close up, the national map for Biden vs Trump:

450.1 days until polls start to close on Election Day 2024.

It has been five weeks since my last post instead of four, but I noticed we were coming up on a milestone, so I waited an extra week.

As I start writing this post, it has been 75 minutes since we passed the 500 day mark until the first states close their polls for Election 2024, and we start seeing real results. It will be a bit less by the time I finish and hit publish, but still, it seemed worth noting.

For those not wanting to read all the details below, here is the TLDR:

• If a Biden vs Trump election was held today, it would be a dead heat and could easily go either way. A ton of critical states are "too close to call".
• Biden has a narrow lead if you take the polls at face value, but given that on average in the last four election cycles polls have tended to underestimate the Republican, I still give Trump a slight edge on the probabilistic view.
• Since November the trend has been in Biden's direction, and this trend has continued in the last month.

OK, now some details:

Since the last post there have been 29 new data points added.

• 16 for Biden vs Trump [NVx2, CAx2, GAx2, KY, TX, IA, VA, NC, WA, MD, MI, AZ, PA]
• 11 for Biden vs DeSantis [TX, IA, NV, NC, WA, CA, MD, MI, AZ, GA, PA]
• 1 for Harris vs Trump [TX]
• 1 for Harris vs DeSantis [TX]

If you want updates on each and every poll as it comes out, as well as daily summaries of the status for the best polled matchup (currently Biden vs Trump), follow Election Graphs on Mastodon.

Let's start again with the "spectrum of close states" for Biden vs Trump.

As it was on the last post on 2023-05-21:

And now on 2023-06-25:

The states where the poll average moved toward Trump are:

• North Carolina: Trump by 0.5% -> Trump by 1.5% (Trump+1.0%)
• Nevada: Biden by 0.4% -> Trump by 0.5% (Trump +0.9%)

And the states where the poll average moved toward Biden are:

• Michigan: Biden by 2.2% -> Biden by 2.3% (Biden+0.1%)
• Pennsylvania: Biden by 1.8% -> Biden by 2.6% (Biden+0.8%)
• Texas: Trump by 6.0% -> Trump by 5.2% (Biden+0.8%)
• Iowa: Trump by 10.0% -> Trump by 9.2% (Biden+0.8%)
• Arizona: Trump by 1.8% -> Trump by 0.6% (Biden+1.2%)
• Georgia: Trump by 0.7% -> Biden by 0.9% (Biden+1.6%)
• Virginia: Biden by 5.6% -> Biden by 8.0% (Biden+2.4%)

Of these there were two that changed categories, so lets take a closer look at those.

In the last update I said this about Nevada:

You can see that what happened here is that what looks like an outlier leaning toward Trump was replaced in the "last five polls" by an outlier that leans toward Biden, thus moving the average significantly toward Biden. But this leaves us JUST BARELY on the Biden side of the fence. The next poll in Nevada could easily flip the state back to the red side. Or it could show that this was no outlier, but a harbinger of a new trend. Too soon to tell.

Basically, the next poll in Nevada flipped the state back to the red side, just as I said might happen. It was another poll that looks like an outlier, this time on the Trump side. The Election Graphs poll averages don't exclude polls, but just glancing at the chart above and using human judgement, I'd probably throw out any of the polls showing either candidate with a lead over 5%. All the other polls show a close race, and all but one of those show a small Trump lead. So if I had to guess the "true" state of Nevada, I'd say there is a narrow Trump lead.

The one caveat would be that if you look at only those non-outlier polls, the rest seem to be trending slowly toward Biden over time. If you mentally draw that trend line, Nevada is actually pretty close to a tie right now. So maybe the real situation is a tie race in Nevada right now, but trending toward Biden.

Georgia doesn't seem to have the same outlier issue as Nevada, but there does seem to have been a shift around the midterms in November 2022.

Before that point, there was only a single poll showing a Biden lead, and most polls didn't just show a Trump lead, they showed a Trump lead of more than 5%.

After the midterms, there has only been a single poll showing a Trump lead, with all of the others showing narrow Biden leads.

So what we are seeing here is the Election Graphs average finally having enough post-midterms polls for the trend line to reflect this change and show a narrow Biden lead, which seems about right for Georgia right now.

The actual poll average right now is an 0.9% Biden lead in Georgia. But based on looking at how Election Graphs poll averages correlated to actual election results from 2008 to 2020, a Democratic lead of 0.9% only translates into a 46.1% chance of the Democrat winning, at least based on that historical performance.

Simply put, more times than not, the polling average has underestimated the Republican, which means the Democrat needs to be leading the poll average by more than 1.3% for me to list them as having a better than 50/50 shot of winning. If anybody wants details of how I calculate that, look at this post from January.

As everyone knows, "past performance is not a guarantee of future results", but looking at past performance is the best I can do.

Bottom line though, Georgia is looking super close at the moment, and like Nevada, could easily go either way if the election was held today. (Which, obviously, it won't be, and things will change a thousand times before we get there.)

OK, so how does all this change the national picture? Here is the current overall summary:

Looking at the evolution of the Biden win odds first:

• 2023-03-25: Between 17.8% and 25.8%
• 2023-04-24: Between 24.9% and 32.3%
• 2023-05-21: Between 34.9% and 35.9%
• 2023-06-25: Between 43.9% and 46.0%

Each month Biden has been stronger than the month before.

Visually, the two odds charts:

Trump still has a slight advantage, but only due to what I mentioned earlier about the Election Graphs polling average tending to underestimate the Republicans in the last few cycles.

Taking that factor into account here is what the trend in the range of possibilities looks like assuming the states are completely independent:

And assuming any polling error will be the same in every state:

Both of these views show Trump with a slight advantage, but with a huge range of possible outcomes very possible. The darker the green, the more likely the outcome is in that range, with the three shades being 1σ (68.27%), 2σ (95.45%), and 3σ (99.73%) probability bands.

In both models above, even the 1σ bands include either candidate winning, so this remains a situation where either candidate could win easily.

Removing the "well, polls have underestimated Republicans in the past" factor and just looking at who is ahead in each state and what the close states are, you get this:

Looking at snapshots of this on the days I've done blog posts:

Categorization Trump Best / Expected / Biden Best:

• 2023-03-25: Trump+96 / Trump+18 / Biden+162
• 2023-04-24: Trump+96 / Trump+18 / Biden+162
• 2023-05-21: Trump+96 / Trump+6 / Biden+162
• 2023-06-25: Trump+96 / Biden+14 / Biden+162

It is easy to just fixate on that middle number moving toward Biden. Unlike the two probabilistic models, Biden is indeed in the lead for the first time since September.

But once again the full picture here is that there is a wide range of reasonably possible options, and we essentially have a tie race right now.

A more subtle way to look at the straight unmodified polls is to look at the "tipping point", which is how much you would have to shift all the polls to change the winner. It has been evolving like this:

• 2023-03-25: Trump by 0.7% in Wisconsin
• 2023-04-24: Trump by 0.5% in North Carolina
• 2023-05-21: Trump by 0.2% in Wisconsin
• 2023-06-25: Biden by 0.9% in Georgia

Once again, this is just another way of showing a very close race, but one that is moving slowly in Biden's direction.

But how does this compare to the last couple of cycles?

So…  yes, things have been moving away from Trump and toward Biden. But Trump is polling better now than he was either 4 or 8 years ago. I've said this before, and I'll say it many more times I'm sure: Nobody should underestimate Trump in this situation.

But what about people other than Trump?

The only other candidate combination with more than scattered polls here and there is Biden vs DeSantis. But the polling at the state level for this combination is still woefully inadequate.

For Biden vs Trump there are enough polls for a full poll average that doesn't rely on old election results as a baseline in every single one of the close states (not counting ME and NE CDs).

For Biden vs DeSantis, the only close states with that much polling are Georgia, Nevada, and Arizona. (DeSantis also has that level of polling in Florida, but while Florida is a close state for Trump, it is not for DeSantis.)

Bottom line, continue to treat Biden vs DeSantis with a big grain of salt until there is a lot more polling. And completely ignore all the OTHER possible combinations. The polling for those is still just completely useless.

Having said that, here is a look at the median case for the independent states model that compares the most polled combinations:

Like I said, ignore everything besides Biden vs Trump and Biden vs DeSantis, and take Biden vs DeSantis with a grain of salt, but…

The recent trend does show that while Trump has been falling vs Biden, DeSantis has been rising. Based on this particular view of the current state level polls, DeSantis would do much better against Biden than Trump would.

Again though, until there are a good number of Biden vs DeSantis polls in all of the close states, I would not completely trust that Biden vs DeSantis picture.

I'm also showing the single chart that shows the best picture for DeSantis here. While DeSantis is improving on the other metrics too, it is nowhere near as dramatic as this one. For full Biden vs DeSantis info, look here.

That is enough for now. As usual, I'll close with the update national map for Biden vs Trump:

I mentioned at the top that there would be less than 500 days left by the time I got the post published. I was right. It is a whole day later. 🙂

499.0 days until polls start to close on Election Day 2024.

It has been been just over four weeks since my last blog post.

Since then on a state level there have been 6 Biden vs Trump polls (NC, IA, PAx2, AZ, MI) along with 5 Biden vs DeSantis polls (NC, IA, PA, AZ, MI), and 1 Biden vs Pence poll (NC). If you want updates on each and every poll as it comes out, as well as daily summaries, follow Election Graphs on Mastodon. Right now the polling volume is still pretty low. It will accelerate as the election gets closer. Eventually there will be tons of new polls every single day. But not for a long while yet.

Honestly the situation isn't all that different than it was four weeks ago. There has been some movement toward Biden, but not a really dramatic change. Just Trump slowly getting a bit weaker. But it has been four weeks, so it seems worth looking at things again.

Let's start by looking at how the "spectrum of close states" has changed:

2023-03-25

2023-04-24

What changes do we see?

• Michigan: Biden by 2.4% -> Biden by 2.2% (Trump+0.2%)
• Pennsylvania: Biden by 1.6% -> Biden by 1.8% (Biden+0.2%)
• North Carolina: Trump by 1.9% -> Trump by 0.5% (Biden+1.4%)
• Arizona: Trump by 4.1% -> Trump by 1.8% (Biden+2.3%)
• Iowa: Trump by 11.0% -> Trump by 10.0% (Biden+1.0%)

So 4 out of 5 states with Biden vs Trump polls moved toward Biden.

None of these changed the picture in my categorization view, but  this does adjust the probabilistic views a bit. Here is the new overall status summary:

Since ties would almost certainly end up going for Trump in the end once it got thrown to the House voting by state delegation, rather than confuse things by having to add those up, I'll look at the odds for Biden:

• 2023-03-25: Biden win odds between 17.8% and 25.8%
• 2023-04-24: Biden win odds between 24.9% and 32.3%

As always, these are "if the election was held today", which it isn't. This still shows Biden as an underdog in this matchup. But doing better than a month ago.

The odds charts:

As usual, the Independent States chart is more dynamic, but these represent extremes, and the "truth" is somewhere in between. And both views still show Trump peaking right around the 2022 midterms, and slowly deteriorating ever since.

Some of that downward movement is after his indictment in NY, but there was even more before that. So at this point you can't really say that event was an inflection point. The already in progress decline just continued.

Oh, and I didn't mention Biden vs DeSantis, or any other combination other than the 2020 rematch, because that is still the only combination with enough state level polling to be able to feel confident about the national picture. Biden vs DeSantis is getting there. But isn't there yet. If you want to look at that combination yourself, here is the Biden vs DeSantis summary.

Not much else to say for the moment. So lets end with the new map:

561.8 days until polls start to close on Election 2024.

Since the last post a week ago where I laid out how things stood using just the last five presidential election results as a starting point, I've gone ahead and ingested all 214 state level presidential data points that are already out there into Election Graphs .

The main thing this tells me? Yes, it is still "super early" to look at 2024 match ups. All kinds of things will change between now and November 2024. But even last year in 2022 there was a lot going on in the polling. So maybe start earlier for the 2028 cycle. 🙂

Let me start with how things look now, then go back to how things seemed to evolve over the last year.

I will be looking specifically at the Biden vs Trump matchup.

That is by far the most polled matchup, and the only one with enough polling to even remotely be able to claim there is a good picture of what all the close states look like. Second is Biden vs DeSantis, but that lags FAR behind in polling volume. You might be able to see a few things by carefully looking at select states where there is polling, but it is hard to get a meaningful national picture. Beyond those two, other matchups only have a smattering of isolated polls, to the point it isn't even useful to look at them at all until or unless there is a lot more polling.

So where does Biden vs Trump stand right now?

Here come the map, the summary stats, and the spectrum of the closest states:

Bottom line, as of March 25th 2023, the state by state polling shows Trump with an advantage.

In terms of the straight up categorization view it is a slight advantage. Only one state (Wisconsin) needs to flip to put Biden in the lead, and Trump leads there by only 0.7% in my average.

Look more carefully at Wisconsin, and you'll see that the 5 poll average contains 4 actual 2024 polls but still includes the 2020 result (Dem+0.6%), one of the 4 polls looks like it may be an outlier to the Republican side, showing a full 10% Trump lead where all the others show a close race.

So this Trump lead looks pretty tenuous.

At the moment though, our two probabilistic views show this translating into pretty good odds for Trump. 72.2% chance of winning with the Uniform Swing view, and up to 80.6% with the Independent States view. The "true" odds are somewhere between these two depending on how strongly polling errors end up correlating between states.

Why is this the case if the straight up polling gives us a very slight Trump lead?

Mainly because of what I outlined in my January post about the math behind how I calculate those probabilities. To summarize, looking at all the final Election Graphs averages from 2008 to 2020 in aggregate as they compared to the actual election results, for the Democratic candidate to have more than a 50/50 shot at winning, being ahead in the polls is not good enough. They have to have more than a 1.2% lead.

So some of those states where Biden is showing a 1%-4% lead are really pretty uncertain, where some of the states Trump is leading by the same margin are more safe than they seem.

Well, at least that is what you get by averaging out the poll errors covering the last four presidential election cycles. As covered in that previous post, each of those four cycles actually looked pretty different in terms of how the errors played out. We have no idea what the 2024 errors will look like. But starting with the range of errors over the last few cycles and the variability between those cycles is as good a guess as we have.

Also, everything on Election Graphs is "if the election was today". The election is not today, and lots and lots will happen between now and then. EG does not provide a forecast. We show how things look right now.

With the status above, you would say that team Biden needs to work hard at shoring up Pennsylvania, Michigan, and New Hampshire where he barely leads, and start pushing hard on the barely red states like Wisconsin. And not to take for granted Georgia, Arizona, and Nevada, which even though Biden won them in 2020, right now are looking red. And Florida may not be as far out of reach as it seems, so maybe don't ignore it.

Looking from the opposite direction, Trump should be playing some defense in those barely red states because they could easily slip away if he doesn't, and he should be going hard after Pennsylvania and Michigan. Etc.

Some of this is all pretty obvious. We have most of the same "swing states" that we have had for the last few election cycles. And both candidates will end up concentrating their efforts there and pretty much ignoring the rest of the country. Because that is how races look under an electoral college system.

Now, let's look at how things have evolved over the last year. you can see a variety of different views of this evolution on the 2024 Electoral College page. For now though, I'll look at the Electoral College Margin chart for the Probabilistic Independent States view. It is one of the two extremes I show for the probabilistic views, specifically one that assumes the polling errors between states are completely independent, which to be clear, we know they are not. But this view is the most dynamic in terms of how it changes with new polls, so is nice for showing how the overall race trends over time:

First just an explanation of the graph. The vertical axis is the Trump minus Biden margin in the electoral college. So if it is positive, that means Trump wins, if it is negative that means Biden wins. The dark green line is the median result in Monte Carlo simulations based on the state averages and the probabilities we described in January. The three bands of color are the ranges of outcomes in the 1σ (68.27%), 2σ (95.45%), and 3σ (99.73%) bands. So, roughly, the closer to the center line of this you are, the more likely that outcome, and as the green gets lighter, the less likely that outcome.

At the far left of the chart the ranges shown are just representing the "last five elections" average I posted about last week. Over the course of 2021 and 2022 the averages in the close states slowly filled in with real 2024 polls, pushing the old elections out of the average. As such, it is hard to tell how much of the "movement" seen above prior to 2023 is actually driven by changes in public opinion versus just the averages filling out. By late 2022 though, most of the close states had five or more actual 2024 polls, and we can start to interpret movement as actual changes in the status of the race.

Ignore the jagged ups and down at small scale, and at a very broad level this tells a story of either Biden weakening and Trump strengthening over the course of 2022, OR just the polling catching up to that position after showing a bluer version of things by starting with the 2004 to 2020 averages. Either way though, the trend toward Trump peaked toward the end of 2022. In fact the peak occurs very close to the 2020 midterms in November.

For the moment anyway, that seems to be the moment where things started to go the other way directionally, and started heading in Biden's direction.

To be clear though, Biden is still behind. All three of the views provided by Election Graphs show Trump in the lead at the moment. But more narrowly than he was right before the midterms.

At the moment things point to another close nail biter of a race, just like 2016 and 2020. The picture we see right now shows a race that could very easily go either way if the election was today, let alone allowing for all the things that could happen over the course of more than a year and a half.

Biden hasn't even officially announced his candidacy yet. We don't know if Trump will be indicted, and if he is, if that will help him or hurt him. We don't know if others like DeSantis will officially run, and how they will do. And who knows, one or both of the front runners could end up having health issues that impact their ability to run. You never know. Plus all the normal back and forth of national and international events.

We have a long way to go.

Specifically, we have 591.0 days until the first polls start to close on Election Day 2024.

Keep checking back here for updates on how things evolve!

Oh, and if you want to see all the notifications for new polls as they get entered, and the status changes those trigger, as well as daily summary stats of the overall situation, follow Election Graphs on Mastodon too: @ElectionGraphs@newsie.social.

[Edit 2023-03-25 23:42 – Slight wording change.]