This is the third in a series of blog posts for folks who are into the geeky mathematical details of how Election Graphs state polling averages have compared to the actual election results from 2008, 2012, and 2016. If this isn’t you, feel free to skip this series. Or feel free to skim forward and just look at the graphs if you don’t want or need my explanations.
You can find the earlier posts here:
Error vs Margin scatterplot
In the last post I ended by mentioning that assuming the error on poll averages was independent of the value of the poll average might not be valid. There are at least some reasonable stories you could tell that would imply a relationship. So we should check.
I've actually looked at this before for 2012. That analysis showed the error on the polls DID vary based on the margin of the poll average. But it wasn't "close states are more accurate". But maybe that pattern was unique to that year.
So I looked at this relationship again now with all the data I have for 2008, 2012, and 2016:
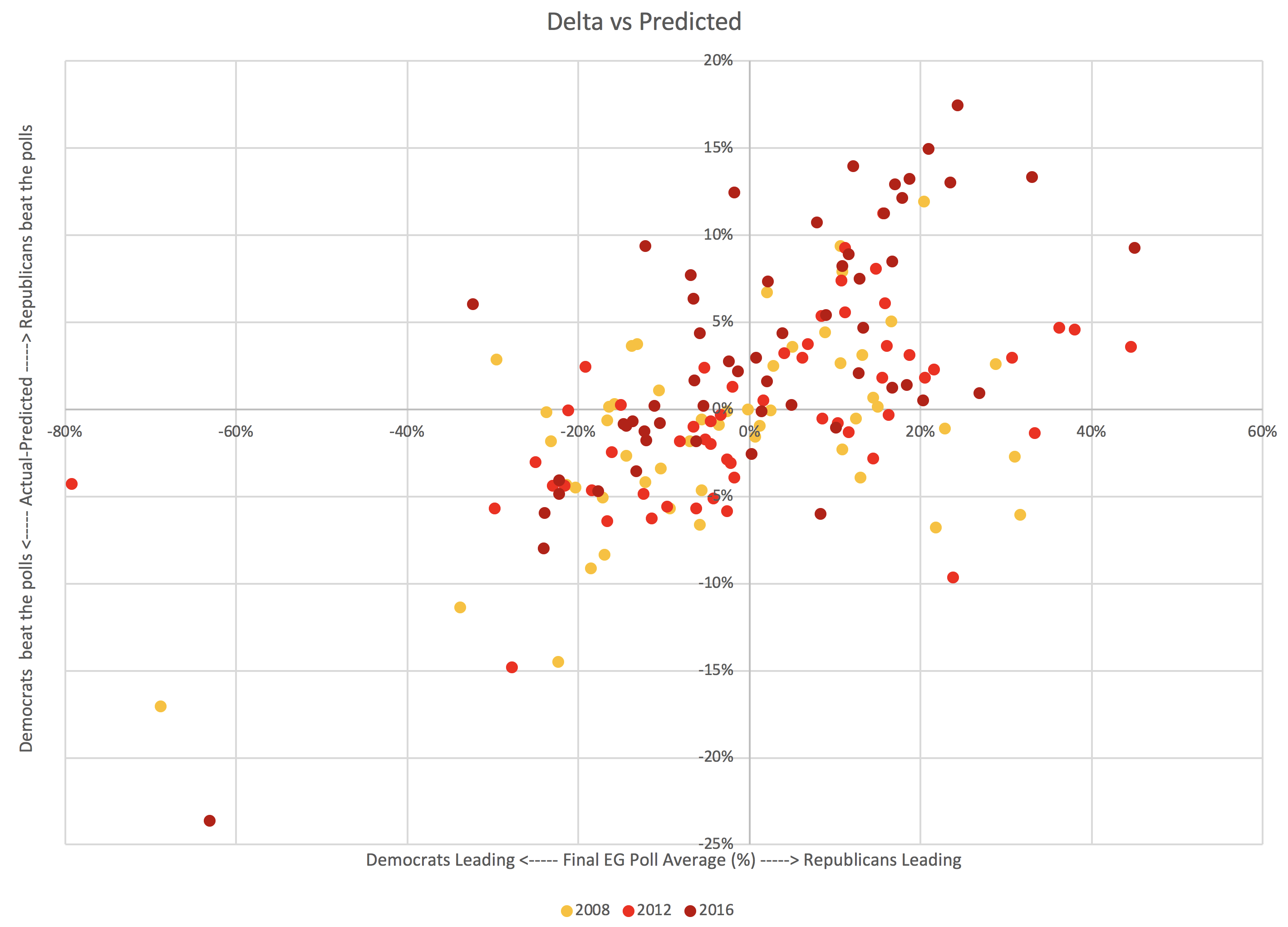
That is just a blob right? Not a scatterplot we can actually see much in? Wrong. There is a bottom left to upper right trend hiding in there.
Interpreting the shape of the blob
Before going further, let's talk a bit about what this chart shows, and how to interpret it. Here are some shapes this distribution could have taken:
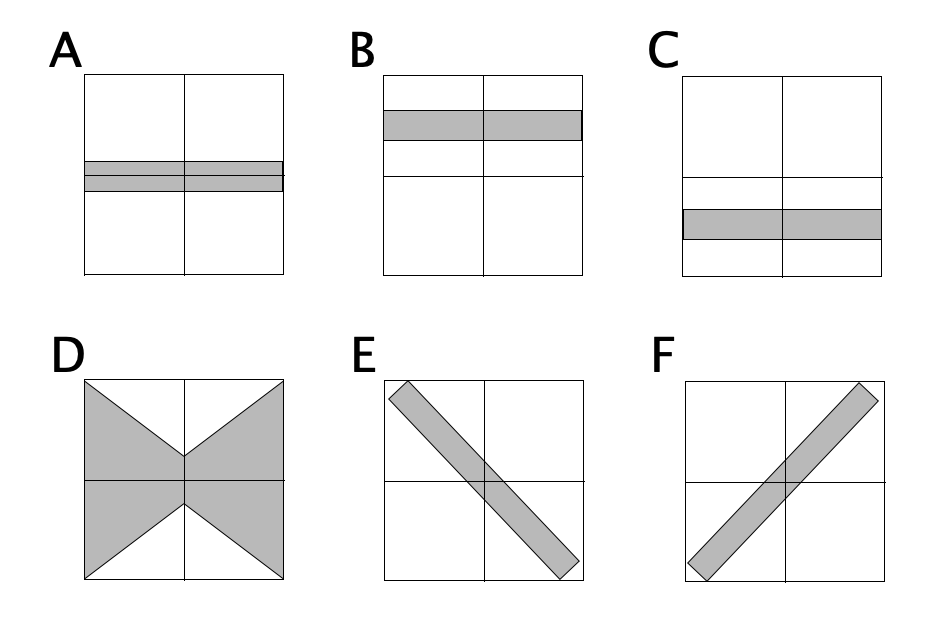
Pattern A would indicate the errors did not favor either Republicans or Democrats, and the amount of error we should expect did not change depending on who was leading in the poll average or how much.
Pattern B would show that Republicans consistently beat the poll averages… so the poll averages showed Democrats doing better than they really were, and the error didn't change substantially based on who was ahead or by how much.
Pattern C would show the opposite, that Democrats consistently beat the poll averages, or the poll averages were biased toward the Republicans. The error once again didn't depend on who was ahead or by how much.
Pattern D shows no systematic bias in the poll averages toward either Republicans or Democrats, but the polls were better (more likely to be close to the actual result) in the close races, and more likely to be wildly off the mark in races that weren't close anyway.
Pattern E would show that when Democrats were leading in the polls, Republicans did better than expected, and when Republicans were leading in the polls, Democrats did better than expected. In other words, whoever was leading, the race was CLOSER than the polls would have you believe.
Finally, Pattern F would show that when the polls show the Democrats ahead, they are actually even further ahead than the polls indicate, and when the Republicans are ahead, they are also further ahead than the polls indicate. In other words, whoever is leading, the race is NOT AS CLOSE as the polls would indicate.
In all of these cases the WIDTH of the band the points fall in also matters. If you have a really wide band, the impact of the shape may be less, because the variance overwhelms it. But as long as the band isn't TOO wide the shape matters.
Also, like everything in this analysis, remember this is about the shape of errors on the individual states, NOT on the national picture.
Linear regressions
Glancing at the chart above, you can determine which of these is at play. But lets be systematic and drop some linear regressions on there…
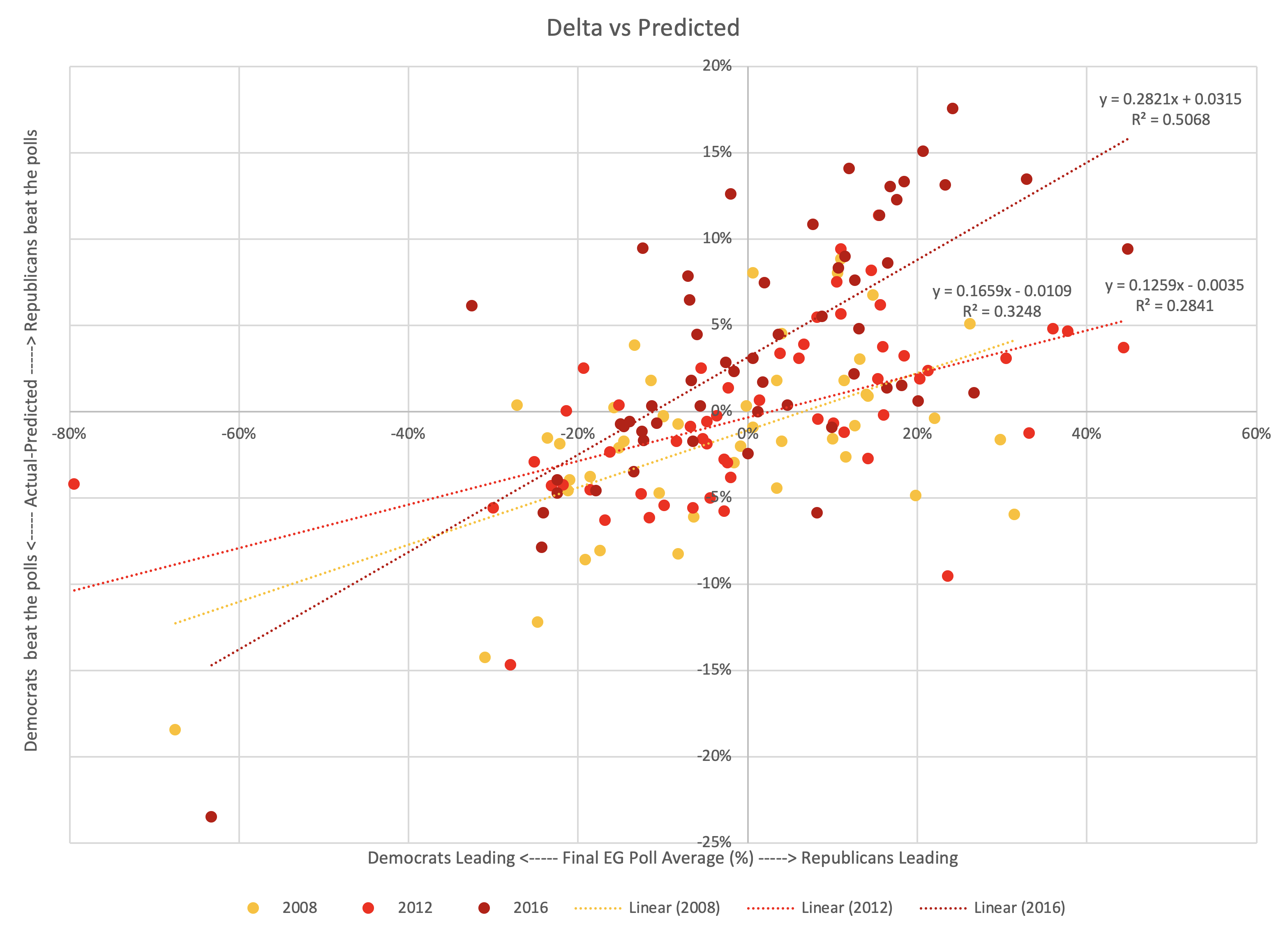
2008 and 2012 were similar.
2016 had a steeper slope and is shifted to the left (indicating that Republicans started outperforming their polls not near 0%, but for polls the Democrats led by less than about 11%). But even 2016 has the same bottom left to top right shape.
I haven't put a line on there for a combination of the three election cycles, but it would be in between the 2008/2012 lines and the 2016 line.
Of the general classes of shapes I laid out above, Pattern F is closest.
Capturing the shape of the blob
But drawing a line through these points doesn't capture the shape here. We can do better. There are a number of techniques that could be used here to get insight into the shape of this distribution.
The one I chose is as follows:
- At each value for the polling average (at 0.1% intervals), collect all of the 163 data points that are within 5% of the value under consideration. For instance, if I am looking at a 3% Democratic lead, I look at all data points that were between an 8% Democratic lead and a 2% Republican lead (inclusive).
- If there are less than 5 data points, don't calculate anything. The data is too sparse to reach any useful conclusions.
- If there are 5 or more points, calculate the average and standard deviation, and use those to define boundaries for the shape.
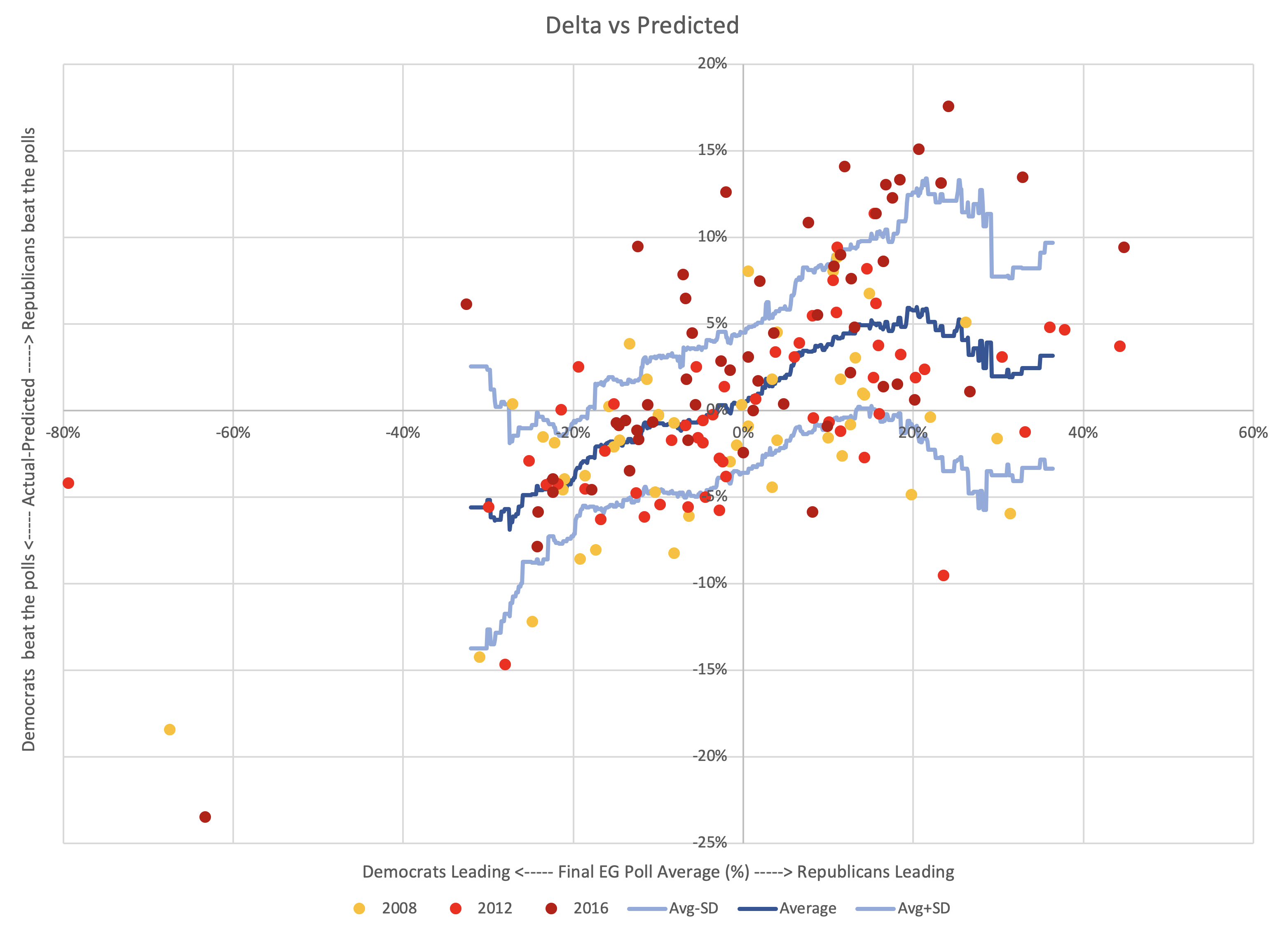
This is a more complex shape than any of the examples I described. Because it is real life messy data. But it looks more like Pattern F than anything else.
It does flatten out a bit as you get to large polling leads, even reversing a bit, with the width increasing like Pattern D, and there some flatter parts too. But roughly, it is Pattern F with a pretty wide band.
Fundamentally, it looks like there IS a tendency within the state level polling averages for states to look closer than they really are.
Is this just 3P and undecided voters?
All of my margins are just "Republican minus Democrat". Out of everybody, including people who say they are undecided or support 3P candidates. But those undecideds eventually pick someone. And many people who support 3rd parties in polls end up voting for the major parties in the end. Could this explain the pattern?
As an example assume the poll average had D's at 40%, R's at 50%, and 10% undecided, that's a 10% R margin… then split the undecideds at the same ratio as the R/D results to simulate a final result where you can't vote "undecided", and you would end up with D's at 44.4% and R's at 55.6% which is an 11.1% margin… making the actual margin larger than the margin in the poll average, just as happens in Pattern F.
Would representing all of this based on share of the 2-party results make this pattern go away?
To check this, I repeated the entire analysis using 2-party margins.
Here, animated for comparison, is the same chart using straight margins and two party margins.
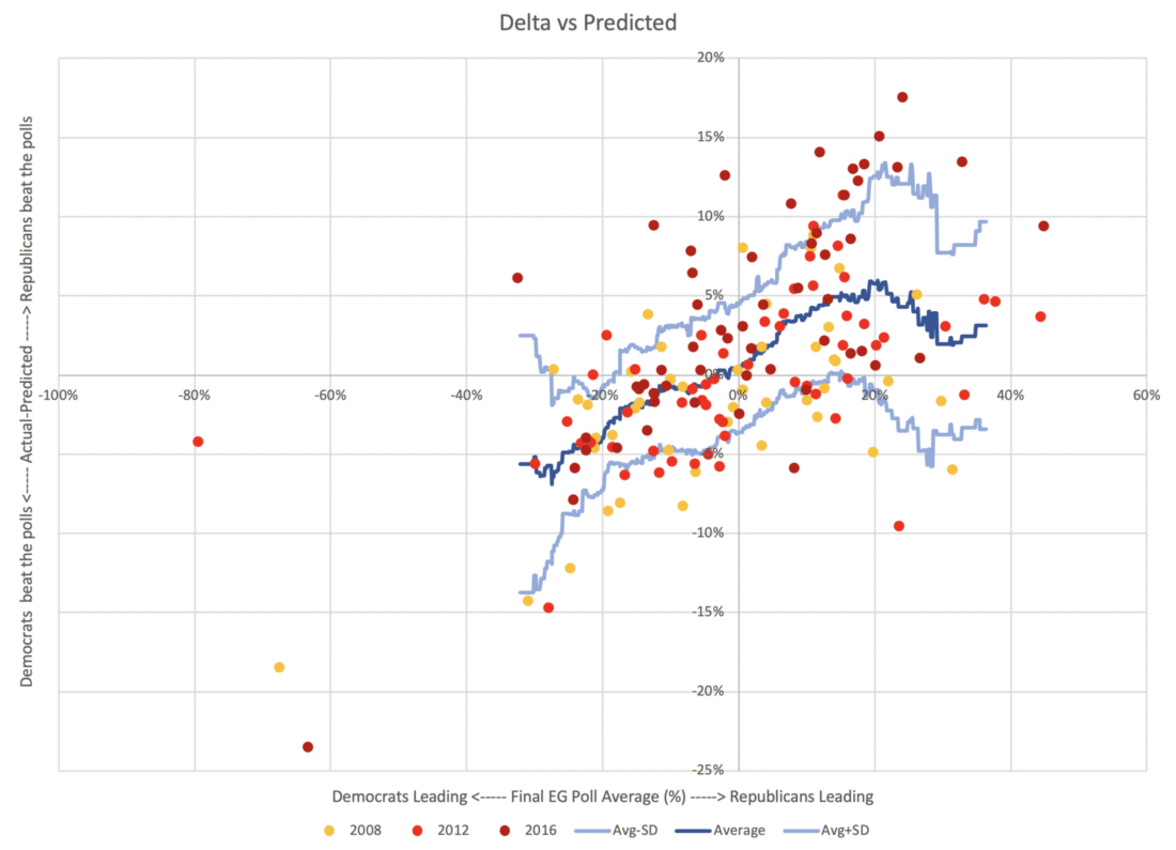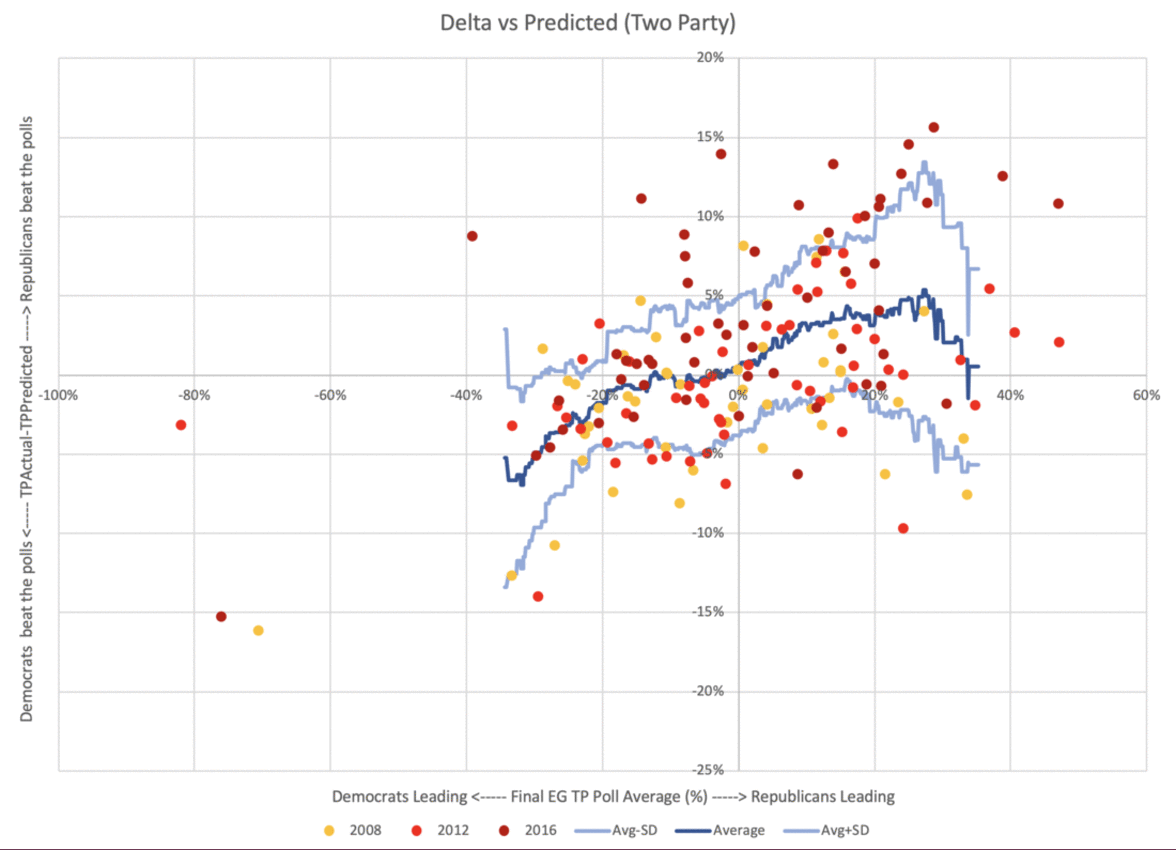
While the pattern is dampened, it does not go away.
It may still be the case that if we were looking at more than 3 election cycles, this would disappear. I guess we'll find out once 2020 is over. But it doesn't seem to be an illusion caused simply by the existence of undecided and 3P voters.
Does this mean anything?
Now why might there be a tendency that persists in three different election cycles for polls to show results closer than they really are? Maybe close races are more interesting than blowouts so pollsters subconsciously nudge things in that direction? Maybe people indicate a preference for the underdog in polls, but then vote for the person they think is winning in the end? I don't know. I don't have anything other than pure speculation at the moment. I'd love to hear some insights on this front from others.
Of course, this is all based on only 3 elections and 163 data points. It would be nice to have more data and more cycles to determine how persistent this patten is, vs how much may just be seeing patterns in noise and/or something specific to these three election cycles. After all, 2016 DID look noticeably different than 2008 and 2012, but I'm just smushing it all together.
It is quite possible that the patterns from previous cycles are not good indicators of how things will go in future cycles. After all, won't pollsters try to learn from their errors and compensate? And in the process introduce different errors? Quite possibly.
But for now, I'm willing to run with this as an interesting pattern that is worth paying some attention to.
Election Result vs Final Margin
Before determining what to do with this information, lets look at this another way. After all, while the amount and direction of the error is interesting, in terms of projecting election results, we only really care if the error gives us a good chance of getting the wrong answer.
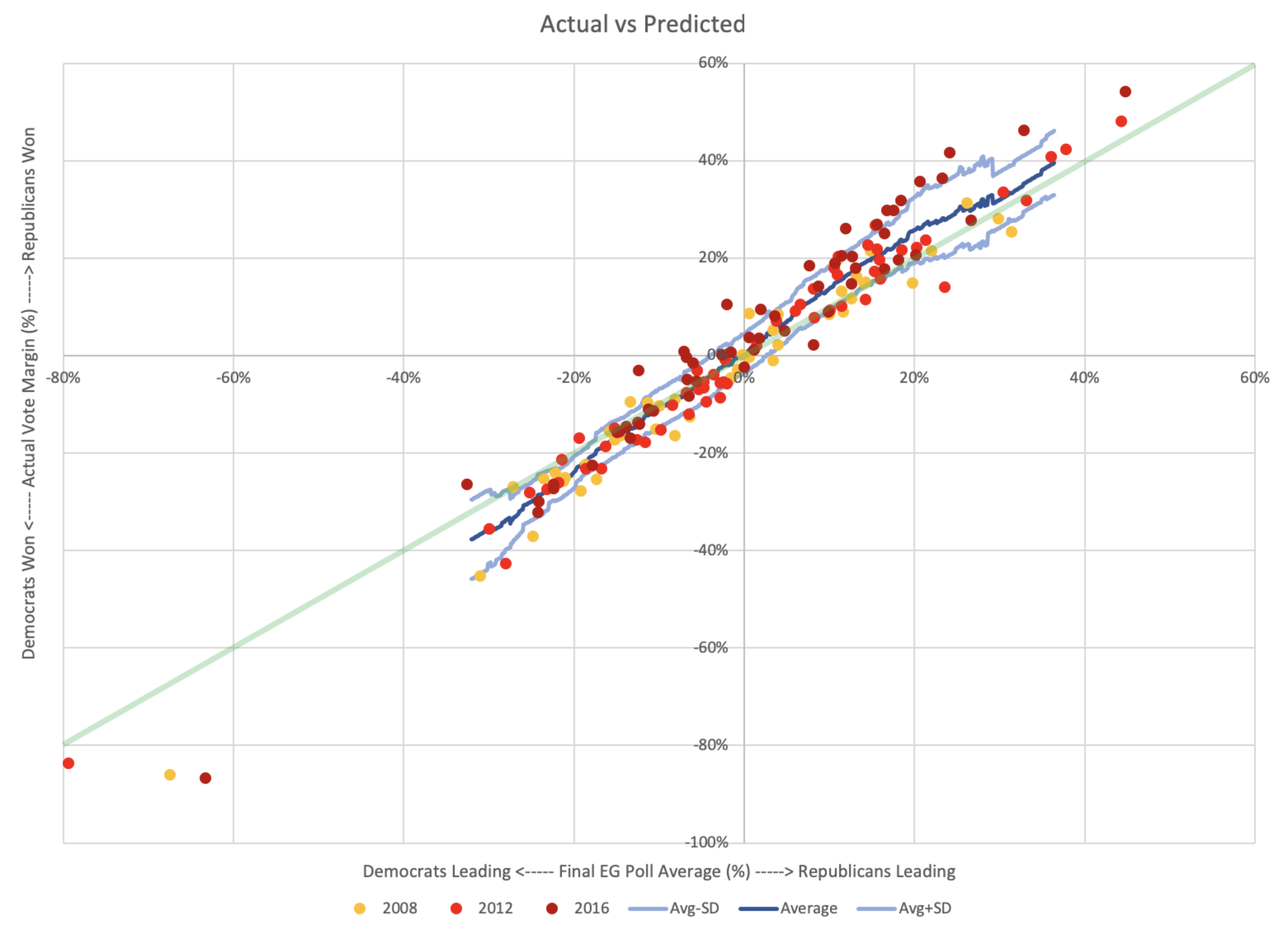
Above is the actual vote margins vs the final Election Graph margins, with means and standard deviations for the deltas calculated earlier plotted as well. Essentially, the first graph is this new second graph with the y=x line (which I have added in light green) subtracted out.
The first view makes the deviation from "fair" more obvious by making an unbiased result horizontal instead of diagonal, but this view makes it easier to see when this bias may actually make a difference.
Lets zoom in on the center area, since that is the zone of interest.
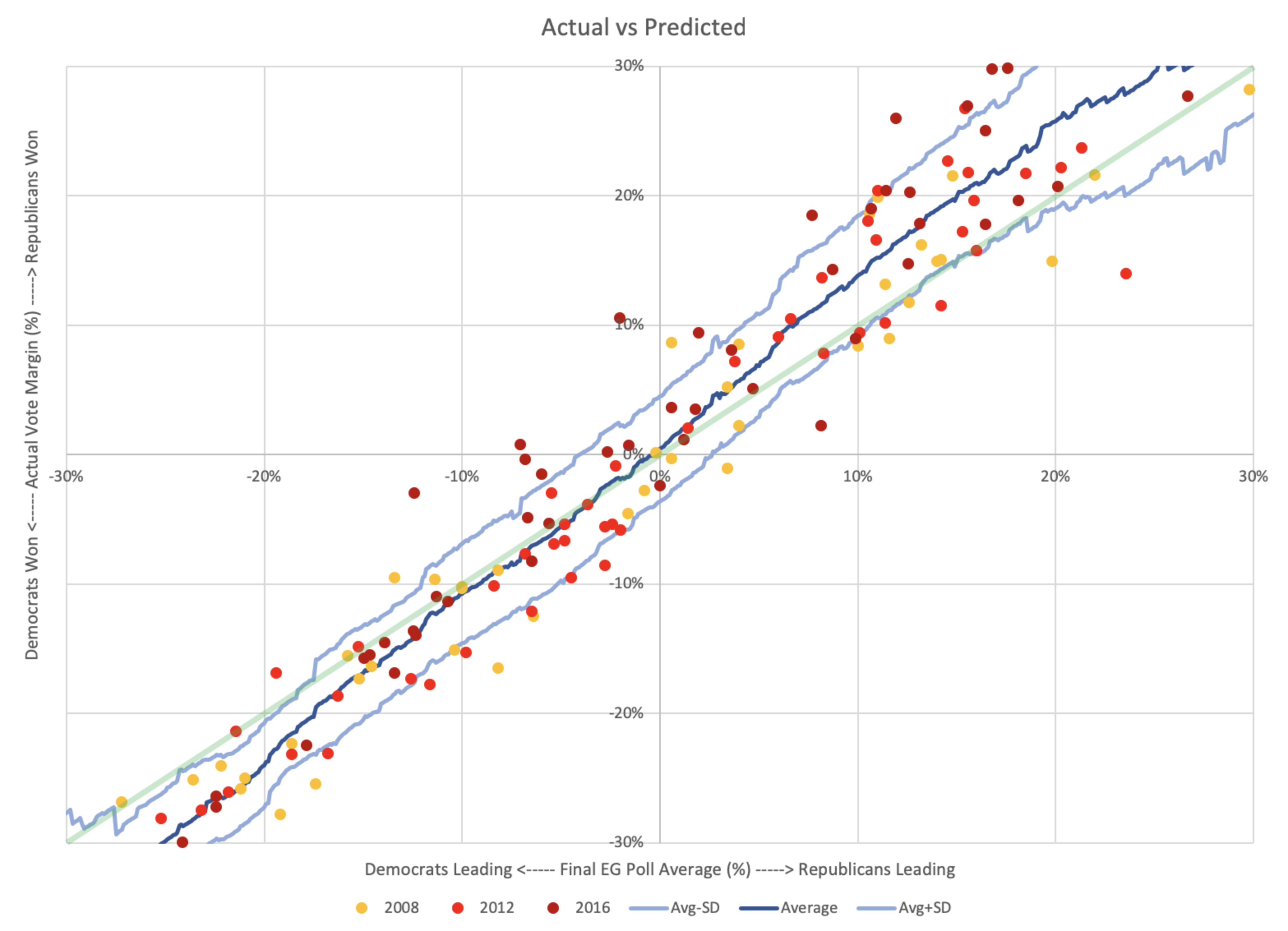
Accuracy rate
Out of the 163 poll averages, there were only actually EIGHT that got the wrong result. Those are the data points in the upper left and lower right quadrants on the chart above. That's an accuracy rate of 155/163 ≈ 95.09%. Not bad for my little poll averages overall.
The polls that got the final result wrong range from a 7.06% Democratic lead in the polls (Wisconsin in 2016) to a Republican lead of 3.40% (Indiana in 2008).
For curiosity's sake, here is how those errors were distributed:
| D's lead poll avg but R's win |
R's lead poll avg but D's win |
Total Wrong |
|
| 2008 | 1 (MO) | 2 (NC, IN) | 3 |
| 2012 | 0 | 0 | 0 |
| 2016 | 4 (PA, MI, WI, ME-CD2) | 1 (NV) | 5 |
| Total | 5 | 3 | 8 |
So, less than 5% wrong out of all the poll averages in three cycles, but at least in 2016, some of the states that were wrong were critical. Oops.
Win chances
Anyway, once we have averages and standard deviations for election results vs poll averages, if we assume a normal distribution based on those parameters at each 0.1% for the poll average, we can produce a chart of the chances of each party winning given the poll average.
Here is what you get:
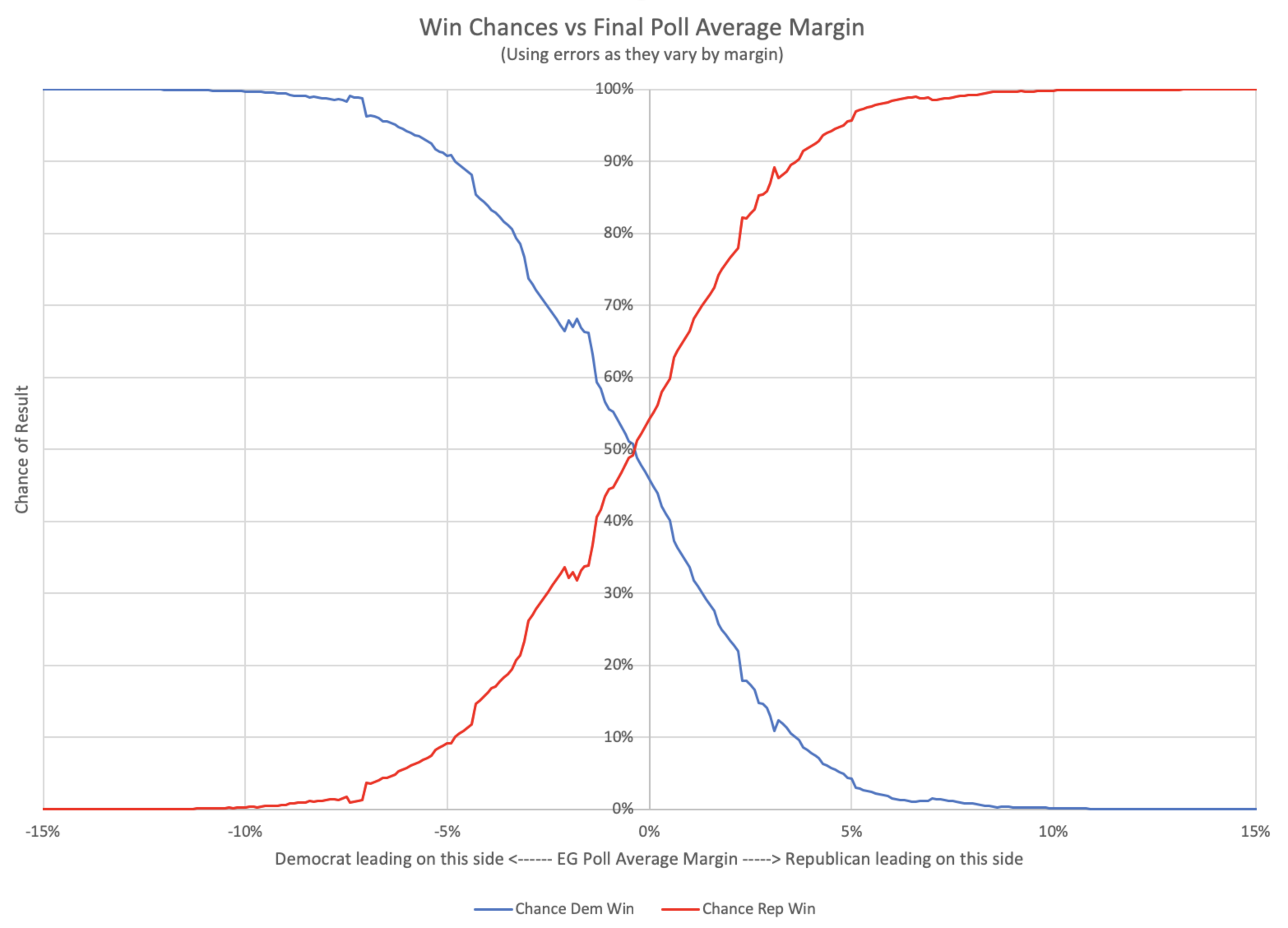
Alternately, we could recolor the graph and express this in terms of the odds the polls have picked the right winner:
You can see that the odds of "getting it wrong" get non-trivially over 50% for small Democratic leads. The crossover point is a 0.36% Democratic lead. With a Democratic lead less than that, it is more likely that the Republican will win. (If, of course, this analysis is actually predictive.)
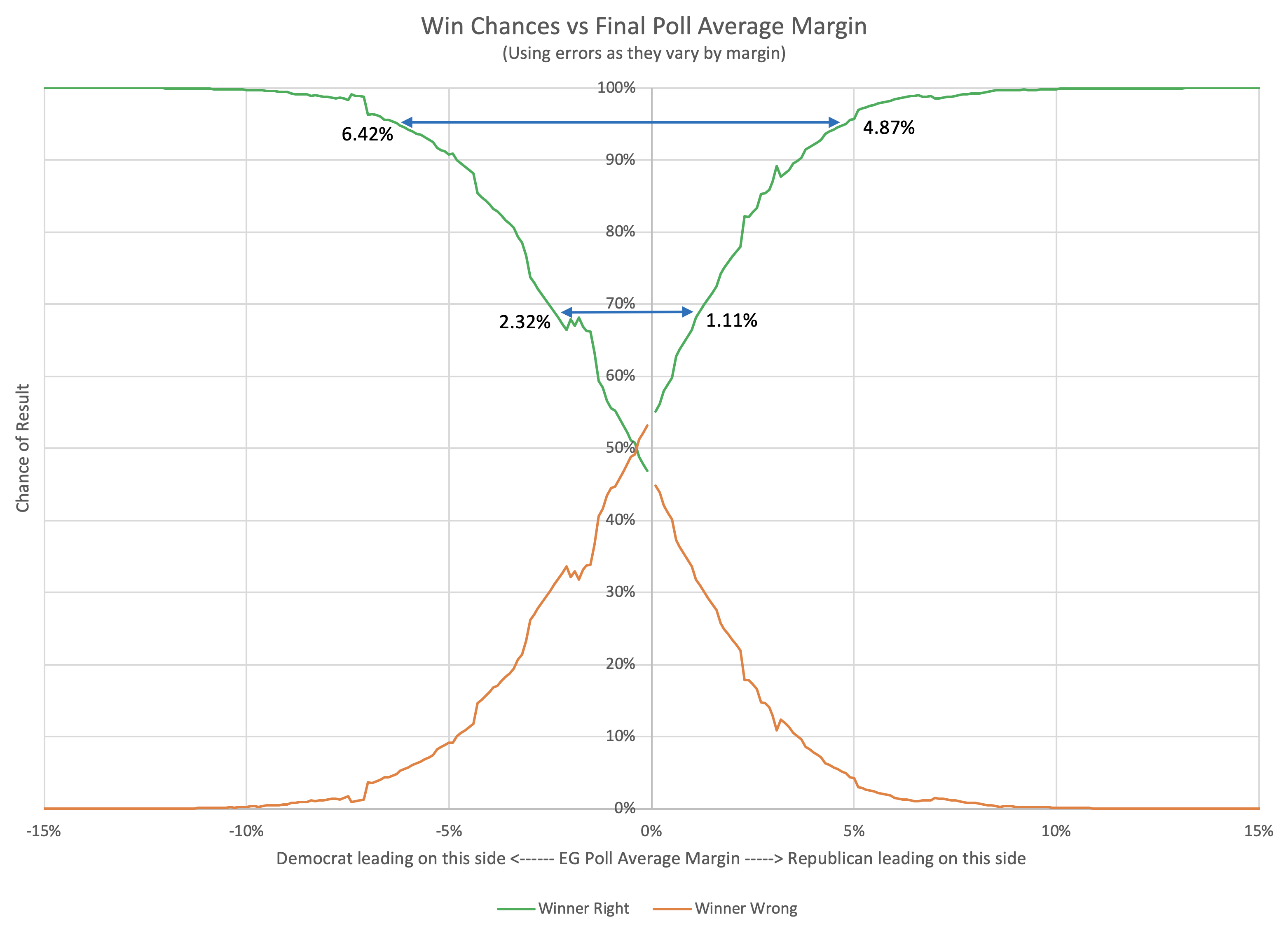
You can also work out how big a lead each party would need to have to be 1σ or 2σ sure they were actually ahead:
| 68.27% (1σ) win chance |
95.45% (2σ) win chance |
|
| Republicans | Margin > 1.11% | Margin > 4.87% |
| Democrats | Margin > 2.32% | Margin > 6.42% |
| Average | Margin > 1.72% | Margin > 5.64% |
Democrats again need a larger lead than Republicans to be sure they are winning.
These bounds are the narrowest from the various methods we have looked at though.
Can we do anything to try to understand what this would mean for analyzing a new race? We obviously don't have 2020 data yet, and I don't have 2004 or earlier data lying around to look at either. So what is left?
Using the results of an analysis like this to look at a year that provided data for that analysis is not actually legitimate. You are testing on your training data. It is self-referential in a way that isn't really OK. You'll match the results better than you would looking at a new data set. I know this.
But it may still give an idea of what kind of conclusions you might be able to draw from this sort of data.
So in the next post we'll take the win odds calculated above and apply them to the 2016 race, and see what looks interesting…
You can find all the posts in this series here:
